Lý thuyết cấp số cộng - Tổng hợp công thức cấp số cộng đầy đủ

Bài tập công thức cấp số cộng là một trong những nội dung quan trọng của toán học, xuất hiện phổ biến trong các bài toán đại số và ứng dụng thực tế. Việc nắm vững lý thuyết cùng các dạng bài sẽ giúp bạn giải bài tập nhanh chóng và hiệu quả. Bài viết dưới đây sẽ tổng hợp toàn bộ lý thuyết cách xác định công sai, công thức tính tổng cấp số cộng để bạn tham khảo.

Lý thuyết cấp số cộng

Đây là một dãy số có tính chất đặc biệt, được ứng dụng rộng rãi trong toán học và thực tiễn. Để hiểu rõ hơn về lý thuyết, chúng ta cần nắm vững các tính chất quan trọng và công thức cấp số cộng. Đây cũng là cơ sở để áp dụng hiệu quả công thức tính tổng cấp số cộng trong các bài toán cụ thể.

Tính chất cấp số cộng

• Hiệu giữa hai số hạng liền kề:

Trong cấp số cộng, hiệu giữa hai số liên tiếp luôn không đổi và được gọi là công sai (ký hiệu d). Nếu a₁, a₂, a₃,…, a_n là một cấp số cộng, thì công thức: 

• Trung bình cộng của hai số hạng bất kỳ:

Trong cấp số cộng, bất kỳ số hạng nào (ngoại trừ số đầu và cuối) đều bằng trung bình cộng của hai số liền kề với nó. Điều này có nghĩa:

Công thức số hạng tổng quát

Công thức này cho phép bạn xác định bất kỳ số nào trong cấp số cộng chỉ cần biết số đầu tiên, công sai và vị trí của số đó. Số hạng tổng quát an của một cấp số cộng được tính bằng công thức:

Trong đó:

• a₁: Số hạng đầu tiên.
• d: Công sai của cấp số cộng, tức là hiệu giữa hai số liên tiếp trong dãy.
• n: Vị trí của số cần tìm trong dãy.

Để học và áp dụng công thức một cách hiệu quả, bạn cần một chiếc laptop mạnh mẽ hỗ trợ việc học tập và tính toán nhanh chóng. CellphoneS hiện cung cấp nhiều dòng laptop với cấu hình tối ưu, giá cả hợp lý, phù hợp cho học sinh nhằm nâng cao hiệu quả giáo dục. Hãy ghé ngay CellphoneS để chọn cho mình một thiết bị học tập hoàn hảo!

[Product_Listing categoryid="380" propertyid="" customlink="https://cellphones.com.vn/laptop.html" title="Danh sách Laptop đang được quan tâm nhiều tại CellphoneS"]

Một số dạng toán cấp số cộng thường gặp

Đây là một chủ đề quen thuộc trong toán học và xuất hiện thường xuyên trong các bài tập từ cơ bản đến nâng cao. Để giải quyết hiệu quả các bài toán liên quan, bạn cần nắm rõ các dạng bài thường gặp. Dưới đây là các dạng toán tiêu biểu về cấp số cộng cùng phương pháp giải:

Dạng 1: Nhận biết cấp số cộng

Đây là bước cơ bản để xác định một dãy số có phải là cấp số cộng hay không. Cần kiểm tra xem hiệu giữa các số liền kề có bằng nhau hay không.

Đề bài: Kiểm tra xem dãy số 2, 5 ,8 ,11 ,14 có phải cấp số cộng không.

Cách giải:
Tính hiệu giữa các số liên tiếp:

5−2=3, 8−5=3, 11−8=3, 14−11=3

Do hiệu giữa các số liên tiếp bằng nhau, đây là một cấp số cộng với công sai d=3.

Dạng 2: Tìm công sai của cấp số cộng

Công sai d là yếu tố quan trọng đặc trưng cho cấp số cộng. Dạng bài này yêu cầu tính giá trị d dựa trên sự chênh lệch giữa hai số liền kề với nhau.

Công thức:

Ví dụ:
Cho cấp số cộng 4,7,10,13,…Tìm công sai.

Lời giải:
Tính d= 7−4 =3 . Vậy đáp án công sai là d=3

Dạng 3: Tìm số hạng của cấp số cộng

Trong dạng bài tập cấp số cộng này, bạn cần xác định một số bất kỳ trong dãy. Để thực hiện điều này, bạn cần áp dụng công thức số hạng tổng quát trong cấp số cộng, cụ thể là:

Công thức:

Ví dụ:
Cho a₁=3, d=5. Tìm số hạng thứ 6.

Lời giải:

a₆ = 3+(6-1)*5= 28

Vậy đáp án là 28.

Dạng 4: Tính tổng n số hạng đầu tiên của dãy

Dạng bài tập cấp số cộng này yêu cầu bạn tính tổng của một số lượng nhất định các số đầu trong dãy số . Công thức để tính tổng n số hạng đầu tiên của dãy được xác định như sau:

Công thức:

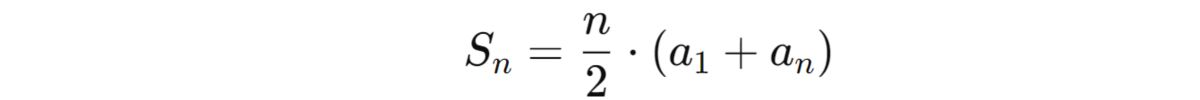
Trong đó:

• S_n là tổng n số đầu tiên
• a₁ là số đầu tiên
• a_n là giá trị thứ n
• n là số lượng các số mà bạn cần tính tổng.

Dạng 5: Tìm cấp số cộng

Dạng bài này yêu cầu bạn dựng lại toàn bộ dãy cấp số cộng từ các thông tin cho trước, chẳng hạn như giá trị đầu tiên, công sai, hoặc tổng của một số lượng nhất định các giá trị. Để giải quyết dạng bài này, bạn cần áp dụng các công thức tính đã học để tính toán các số tiếp theo hoặc tìm công sai từ các dữ liệu đã cho.

Đề bài: Cho a₁= 1, d= 3. Viết 5 số đầu tiên của cấp số cộng.

Lời giải:
Sử dụng công thức an=a1+(n−1)*d

• a₁=1
• a₂=1+3=4
• a₃=1+2*3=7
• a₄=1+3*3=10
• a₅=1+4*3=13
• Vậy dãy số là 1,4,7,10,13.

Ví dụ bài tập tính cấp số cộng

Dưới đây là một số ví dụ về bài tập cấp số cộng để bạn áp dụng công thức tính để thực hành: 

• Bài tập 1: Nhận biết 

Đề: Kiểm tra xem dãy số 1,4,7,10,13 có phải cấp số cộng không.

Giải:

4 - 1 = 3

7 - 4 = 3

10 - 7 = 3

13 - 10 = 3

Vì hiệu giữa các số liên tiếp luôn bằng 3, dãy số này là một cấp số cộng.

• Bài tập 2: Tìm công sai 

Đề: Cho dãy 3,6,9, 12. Tìm công sai.

Giải: 

6 - 3 = 3

9 - 6 = 3

12 - 9 = 3

Vậy công sai d=3d = 3d=3.

• Bài tập 3: Tìm số hạng 

Đề: Cho a₁=5, d=2. Tìm số hạng thứ 10.

Giải:

a₁₀=5+(10−1)*2= 5+18=23

• Bài tập 4: Tính tổng n số hạng đầu tiên của dãy

Đề: Cho a₁=2, d=3. Tính tổng 8 số hạng đầu tiên.

Giải:

Trước tiên, ta tính giá trị thứ 8 (a8):

a₈= a₁+(8−1)*d= 2+7*3= 2+21= 23

Sau đó áp dụng công thức , tính tổng 8 số đầu tiên:

S₈ = 82*(2+23)= 4* 25= 100

• Bài tập 5: Tìm cấp số cộng

Đề: Cho a₁=4, d=2. Viết 3 số hạng đầu tiên của cấp số cộng.

Áp dụng công thức số hạng tổng quát:

a₁ =4

a₂ = a₁+d = 4+2=6

a₃ = a₂+d = 6+2=8

Vậy 3 số đầu tiên của cấp số cộng là: 4, 6, 8

Việc hiểu rõ cách xác định công sai, công thức, bài tập của cấp số cộng sẽ giúp bạn giải quyết các bài toán hiệu quả. Công thức tính tổng cấp số cộng là công cụ tuyệt vời để củng cố kiến thức và nâng cao kỹ năng giải toán. Hãy thường xuyên luyện tập để thành thạo các dạng bài tập này!

Xem thêm bài viết trong chuyên mục: Góc Học & Dạy 4.0