Công thức Heron là gì? Định nghĩa, cách dùng và bài tập ví dụ

Tính diện tích tam giác bằng công thức Heron là phương pháp thông dụng trong hình học, dựa trên độ dài ba cạnh. Không chỉ dùng để giải toán mà nó còn rất hữu dụng khi được áp dụng tốt trong những lĩnh vực khác. Hãy cùng tìm hiểu chi tiết định nghĩa, nội dung và giải các bài tập công thức Heron để nắm vững kiến thức và cách sử dụng!
Công thức Heron tính diện tích tam giác
Trong hình học, công thức Heron là một công cụ mạnh mẽ cho phép tính diện tích tam giác một cách trực tiếp chỉ bằng độ dài ba cạnh của nó. Đây là một phương pháp tiện lợi để xác định diện tích tam giác trong trường hợp thiếu thông tin về chiều cao.
Người ta cũng có thể tận dụng nó để tính diện tích tứ giác. Cách làm là chia tứ giác làm hai tam giác rồi tính diện tích từng tam giác dựa trên các cạnh, sau đó cộng lại.
Nội dung cụ thể:
Cho tam giác mà độ dài ba cạnh được biết là a, b và c. Diện tích S của nó sẽ được tính theo công thức sau:
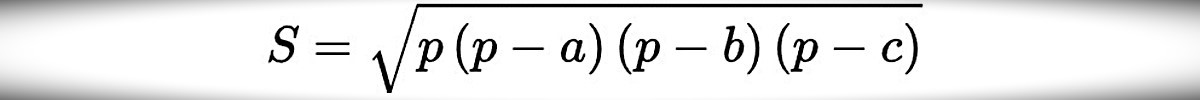
Trong đó:
- a, b, c lần lượt biểu thị độ dài các cạnh của tam giác
- p là nửa chu vi tam giác, được tính theo: p = (a+b+c)/ 2
- S là diện tích của tam giác
Ngoài ra, công thức Heron còn có thể được biểu diễn dưới dạng khai triển như hình dưới đây. Dạng này phức tạp hơn nên thường được dùng trong các ứng dụng toán học và lập trình thay vì giải toán thường.

Lưu ý: Một lưu ý cực kỳ quan trọng là phương pháp Heron chỉ cho kết quả chính xác khi ba giá trị cạnh là a, b, c thực sự tạo thành một tam giác hợp lệ. Điều này được đảm bảo bởi bất đẳng thức tam giác: tổng độ dài của hai cạnh bất kỳ của tam giác phải lớn hơn độ dài cạnh còn lại.
Hiện nay, với kho bài giảng trực tuyến phong phú, học sinh, sinh viên có thể dễ dàng tự học và tra cứu chỉ với một chiếc laptop. Từ việc tìm hiểu định nghĩa công thức Heron, cách áp dụng đến giải các bài tập ví dụ, mọi kiến thức đều nằm trong tầm tay. Hãy sở hữu ngay một chiếc laptop mạnh mẽ để học tập chủ động, hiệu quả và sáng tạo hơn trong giáo dục!
[Product_Listing categoryid="380" propertyid="" customlink="https://cellphones.com.vn/laptop.html" title="Danh sách Laptop đang được quan tâm nhiều tại CellphoneS"]
Cách áp dụng công thức Heron tính diện tích tam giác
Trong nhiều trường hợp, công thức này sẽ làm bài toán của bạn đơn giản đi rất nhiều. Ngay cả khi chỉ biết giá trị ba cạnh, bạn cũng có thể tìm ra diện tích một cách chính xác. Dưới đây là hướng dẫn cụ thể cách tính diện tích tam giác bằng công thức Heron, giúp bạn áp dụng ngay vào các bài tập.
Bước 1: Xác định độ dài ba cạnh (Nếu độ dài chưa được cho, cần đo hoặc tính toán thêm để tìm ra chúng)
Bước 2: Tính nửa chu vi bằng cách lấy tổng độ dài ba cạnh chia đôi: p = (a+b+c)/ 2 ( với p là nửa chu vi; a,b,c đại diện lần lượt cho các cạnh)
Bước 3: Sử dụng công thức Heron để tìm diện tích tam giác
Sau đây là một số ví dụ cụ thể để bạn có thể hình dung cách làm dễ dàng hơn:
Ví dụ 1: Tam giác BCD có độ dài các cạnh BC = 13cm, BD = 14cm, CD = 15cm. Tính diện tích của tam giác này.
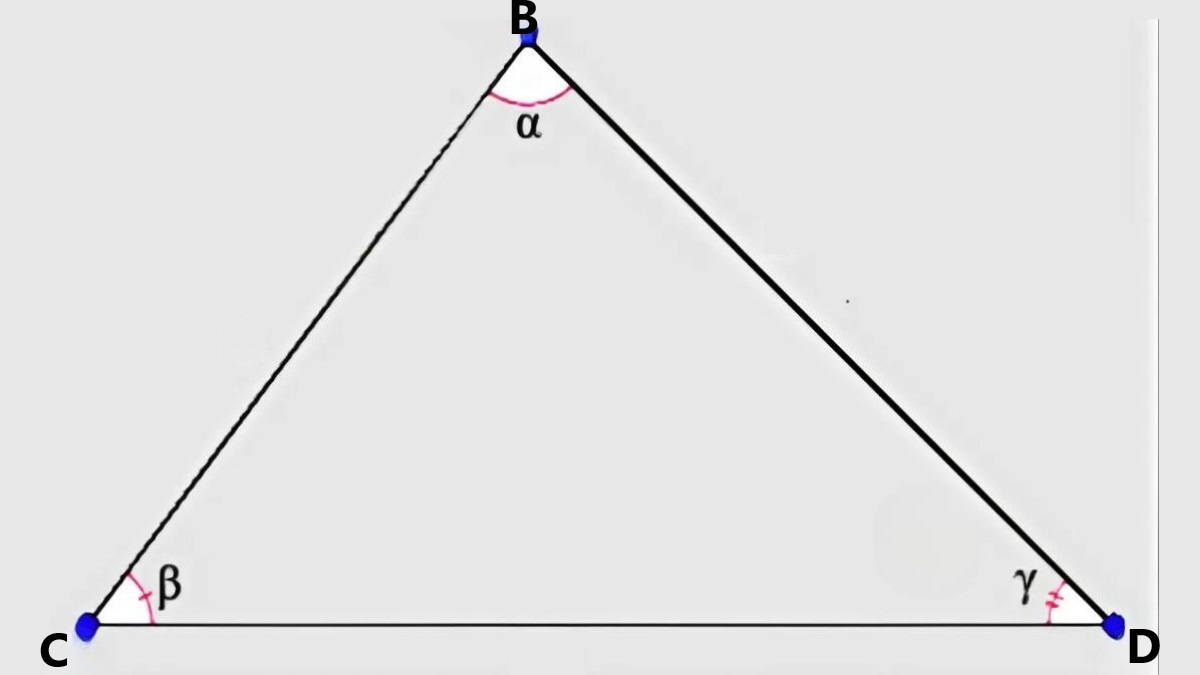
Giải:
Nửa chu vi của tam giác BCD là:
p = (13+14+15)/ 2 = 21 (cm)
Tam giác BCD có diện tích là:
S=√[21(21-13)(21-14)(21-15)]
S=√21 x 8 x 7 x 6
S=√7056
S=84 (cm²)
Ví dụ 2: Một khu vườn hình tam giác có ba cạnh lần lượt là 5m, 6m và 7m, hỏi diện tích khu vườn là bao nhiêu?
Giải:
Nửa chu vi của khu vườn là:
p = (5+6+7)/ 2 = 9 (m)
Diện tích khu vườn được tính như sau:
S =√[9(9-5)(9-6)(9-7)]
S =√9 x 4 x 3 x 2
S =√216
S = 14.7 (m²)
Một số bài tập về công thức Heron
Dưới đây là một số bài tập công thức Heron giúp bạn hiểu rõ hơn khi áp dụng vào giải toán. Các bài tập này tập trung vào việc tính diện tích tam giác bằng công thức Heron trong nhiều trường hợp khác nhau. Cùng xem qua và luyện tập để biết cách áp dụng vào bài nhé!
Bài 1: Một tam giác có chu vi là 48cm và độ dài hai cạnh lần lượt là 15cm và 17cm. Tính diện tích tam giác đó.
Giải:
Gọi cạnh còn lại là x, ta có: 15 + 17 + x = 48 => x = 16 (cm)
Tính nửa chu vi: p = 48/ 2 = 24 (cm)
Diện tích tam giác đó là:
S=√[24(24-15)(24-17)(24-16)]
S=√24 x 9 x 7 x 8
S=√12096
S=109.9 (cm²)
Bài 2: Hãy tìm diện tích của tam giác ABC, biết rằng tọa độ các đỉnh lần lượt là A(1;-1), C(6;0), và B(3;-3).
Giải:


Bài 3: Hình chữ nhật ABCD có độ dài cạnh AB là 4 đơn vị và BC là 6 đơn vị. Điểm M là trung điểm của cạnh BC, và điểm N nằm trên cạnh CD sao cho độ dài đoạn ND gấp ba lần độ dài đoạn NC. Tính diện tích của tam giác AMN.
Giải:
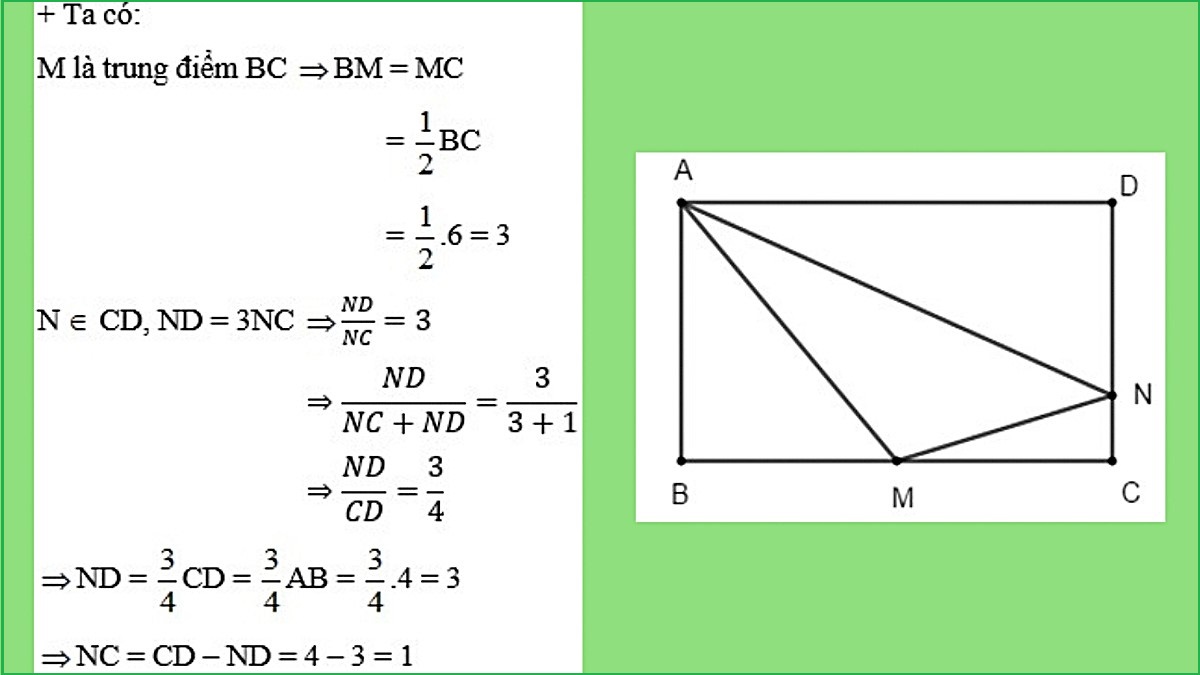


Bài 4: Biết độ dài ba đường trung tuyến của tam giác ABC lần lượt là ma= 15, mb= 12 và mc = 9, xác định diện tích tam giác.
Giải:




Ứng dụng của công thức Heron trong thực tiễn
Không chỉ là những bài tập công thức heron trên sách vở, biểu thức toán học này còn giúp ta giải quyết nhiều vấn đề trong đời sống. Những ứng dụng này có mặt trong xây dựng, thiết kế, và khảo sát địa lý. Việc tính diện tích tam giác bằng công thức Heron có thể mang lại nhiều lợi ích trong công việc hàng ngày, cụ thể như sau:
- Thiết kế công trình: Trong xây dựng, phương pháp Heron giúp tính diện tích các khu vực hình tam giác như mảnh đất, nền móng hoặc mái nhà. Đây là một phương pháp hiệu quả khi không thể đo chiều cao của tam giác, và cũng giúp ước tính vật liệu và chi phí xây dựng.
- Đo đạc và vẽ bản đồ: Các nhà đo đạc và các kỹ sư địa lý sử dụng Heron để tính diện tích các vùng đất trong quá trình vẽ bản đồ. Khi vẽ bản đồ địa lý hoặc địa chính, những khu vực có hình tam giác sẽ cần tính toán diện tích một cách chính xác.
- Nông nghiệp: Trong nông nghiệp, việc tính diện tích các cánh đồng hình tam giác giúp nông dân ước tính lượng phân bón, thuốc trừ sâu cần thiết,... Qua đó, dự đoán năng suất cây trồng, tối ưu chi phí và lên kế hoạch sản xuất hiệu quả hơn.

- Hướng dẫn học tập: Định lý Heron được sử dụng nhiều khi giải toán hình học, giúp học sinh tính diện tích dễ dàng. Đặc biệt là trong các bài toán phức tạp, cần nhiều bước giải, sử dụng phương pháp Heron có lẽ sẽ gỡ được nút thắt.
Tính diện tích tam giác bằng công thức Heron giúp giải quyết nhiều bài toán hình học khó nhằn. Đừng ngần ngại áp dụng kiến thức từ các bài tập công thức Heron vào giải quyết các bài toán thực tế. Bạn sẽ thấy nhiều ứng dụng hữu ích không chỉ trong học tập mà còn trong nhiều lĩnh vực khác.
Xem thêm bài viết trong chuyên mục: Góc Học & Dạy 4.0







Bình luận (0)