Định lý Viet và những ứng dụng, bài tập liên quan

Bạn gặp khó khăn với những phương trình bậc hai phức tạp? Định lý Viet sẽ giúp bạn xử lý chúng một cách nhanh chóng và dễ dàng. Không chỉ hỗ trợ giải phương trình, định lý này còn mang đến nhiều ứng dụng hữu ích trong các lĩnh vực toán học khác. Hãy cùng Sforum khám phá sâu hơn về định lý Viet đảo, lớp 9, tổng quát, bậc 2, bậc 3 và cách áp dụng nó, đừng bỏ qua nhé.

Tìm hiểu về định lý Viet

Định lý Viet là một hệ thức hữu ích trong toán học, đặc biệt hỗ trợ đắc lực trong việc giải các bài toán liên quan đến phương trình bậc hai. Được phát triển bởi nhà toán học người Pháp François Viet, định lý này không chỉ giúp tìm ra mối quan hệ giữa các nghiệm của phương trình, mà còn mở ra nhiều ứng dụng trong các lĩnh vực khác như đại số và lý thuyết số. Hãy cùng tìm hiểu về định lý Viet tổng quát, cách áp dụng nó vào các bài toán thực tế cũng như những ví dụ minh họa chi tiết để nắm vững lý thuyết quan trọng này nhé.

Định lý thuận

Định lý Viet là một công cụ thiết yếu trong việc giải quyết các bài toán về phương trình bậc hai. Công thức này giúp tìm mối quan hệ giữa các nghiệm và các hệ số của phương trình, qua đó rút ra những kết luận có ý nghĩa và hữu ích. Ứng dụng của định lý Viet thuận rất rộng rãi, từ việc giải phương trình nhanh chóng đến việc xây dựng các phương trình mới dựa trên các điều kiện cho trước.

Định lý Viet đảo

Đây là một công cụ quan trọng trong toán học, giúp chúng ta xây dựng phương trình bậc hai khi đã biết tổng và tích của các nghiệm. Ngược lại với định lý Viet thuận, định lý đảo giúp chúng ta xây dựng phương trình từ kết quả. Đây là một mối liên hệ quan trọng, mở rộng khả năng giải quyết các bài toán liên quan đến phương trình bậc hai.

Ứng dụng của định lý Viet

Định lý Viet không chỉ có ích trong việc giải toán học thuần túy mà còn ứng dụng rộng rãi trong các lĩnh vực như điện tử, kỹ thuật và kinh tế học. Khi cần giải quyết các bài toán tối ưu hóa hay mô hình hóa các quá trình phức tạp. Việc áp dụng định lý Viet mang đến những giải pháp đơn giản và hiệu quả trong nhiều bài toán thực tế.

Định lý Viet tại các bậc phương trình

Không chỉ áp dụng cho phương trình bậc hai, định lý Viet còn mở rộng và phát huy hiệu quả với các phương trình bậc cao hơn. Từ việc tính tổng và tích nghiệm đến phân tích đặc điểm của đồ thị, định lý này mang lại nhiều ứng dụng hữu ích trong giải toán và thực tế. Hãy cùng tìm hiểu sâu về vai trò của định lý Viet trong việc giải quyết các phương trình bậc khác nhau.

Bạn có thể khám phá thêm về định lý Viet lớp 9 và các bậc phương trình thông qua các trang web hoặc tài liệu toán học. Tham khảo ngay những mẫu điện thoại tại CellphoneS để hỗ trợ việc tự học hiệu quả và tiện lợi hơn nhé.

[Product_Listing categoryid="3" propertyid="" customlink="https://cellphones.com.vn/mobile.html" title="Danh sách điện thoại đang được quan tâm nhiều tại CellphoneS"]

Định lý Viet bậc 2

Định lý Viet bậc 2 là một phương pháp hữu ích trong việc giải quyết các bài toán, đặc biệt khi tìm nghiệm của phương trình bậc 2 dạng ax² + bx + c = 0 (Với a#0). Theo đó nếu hai nghiệm của phương trình là x₁ và x₂, ta có:

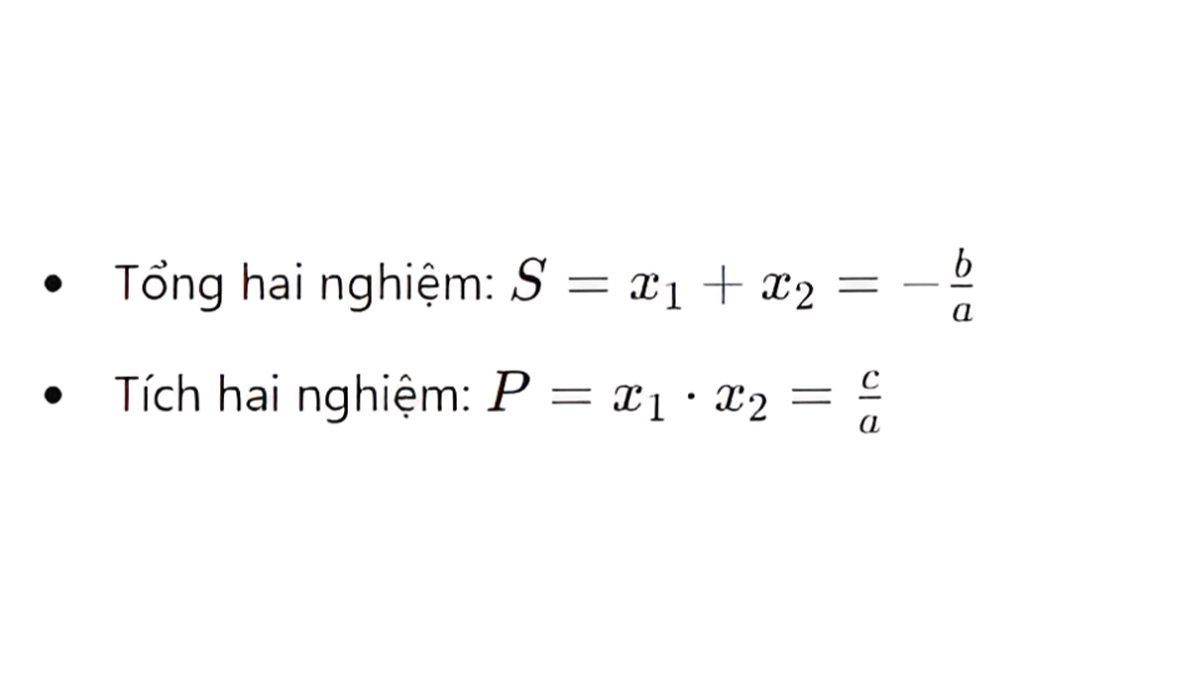
Định lý Viet bậc 2 giúp tính nhanh nghiệm, kiểm tra đáp án và phân tích bài toán một cách hiệu quả. Đây là kiến thức nền tảng cần thiết trong các kỳ thi và ứng dụng thực tế.

Định lý Viet bậc 3

Định lý Viet bậc 3 giúp xác định mối quan hệ giữa nghiệm và hệ số của phương trình bậc 3 một cách nhanh chóng và chính xác. Đối với phương trình dạng ax³ + bx² + cx + d = 0, nếu có ba nghiệm x₁, x₂, x₃ thì định lý Viet cho ta:

Định lý này thường được áp dụng trong giải toán đại số, tìm nghiệm nhanh chóng và phân tích các bài toán liên quan đến đồ thị hàm số. Áp dụng định lý này không chỉ giúp rút ngắn thời gian giải bài toán mà còn nâng cao độ chính xác trong việc tìm nghiệm của phương trình.

Định lý Viet của phương trình đa thức bất kỳ

Đối với phương trình đa thức bậc n có dạng:

P(x) = a_nxⁿ + a_n-1x^n-1 + … + a₁x + a₀ = 0

Giả sử các nghiệm của phương trình này là x₁ x₂,..., x_n thì ta có công thức sau:

Và các công thức tương tự cho tổng các tích bậc cao của nghiệm. Định lý Viet là công cụ hữu ích giúp giải phương trình đa thức và xác định nghiệm mà không cần giải trực tiếp.

Các ứng dụng quan trọng của định lý Viet

Định lý Viet tổng quát không chỉ là một lý thuyết toán học cơ bản, mà còn mang lại nhiều ứng dụng thực tiễn đầy giá trị và hữu ích. Dưới đây là một số ví dụ phổ biến được áp dụng trong các bài toán tổng quát:

• Tính tổng và tích các nghiệm trực tiếp từ các hệ số của phương trình.
• Giúp giải quyết các bài toán trong lĩnh vực chuyển động, vật lý và kinh tế có liên quan đến phương trình bậc hai.
• Xác định nghiệm phương trình nhanh chóng mà không cần phải giải chi tiết.
• Dùng tổng và tích nghiệm để suy luận về tính chất đồ thị hàm số bậc hai.

Một số bài tập áp dụng

Một số bài tập về cách ứng dụng định lý Viet mà bạn có thể tham khảo:

Bài tập 1: Tìm hai nghiệm của phương trình bậc hai biết tổng và tích

Đề bài: Tìm phương trình bậc hai biết tổng nghiệm x₁ + x₂ = 5 và tích nghiệm x₁ . x₂ = 6

Bài tập 2: Chứng minh một mối quan hệ giữa các nghiệm

Ta có bài tập như sau: 

Bài tập 3: Xác định điều kiện của nghiệm

Đề bài: Cho phương trình x₁ - px + q = 0. Xác định điều kiện của p,q để hai nghiệm x₁ , x₂ thỏa mãn x₁ > 0 và x₂ > 0

Định lý Viet không chỉ hỗ trợ việc giải phương trình bậc hai một cách hiệu quả mà còn cung cấp những ứng dụng quan trọng trong việc giải các bài toán đại số. Việc nắm vững định lý Viet đảo, lớp 9, tổng quát, bậc 2, bậc 3 và cách áp dụng sẽ giúp bạn tiết kiệm thời gian, đồng thời tăng cường khả năng tư duy logic và kỹ năng giải toán. Hy vọng qua những bài tập và ví dụ minh họa, bạn sẽ hiểu rõ hơn về định lý này và có thể vận dụng linh hoạt trong học tập cũng như các kỳ thi nhé.

• Theo dõi các kiến thức mới nhất về Toán học tại chuyên mục: Giáo dục; Góc Học & Day 4.0