Giải mã nguyên hàm ln x là gì - Định nghĩa và cách tính

Giang Nguyễn, Tác giả Sforum - Trang tin công nghệ mới nhất

Ngày đăng: 15/03/2025-Cập nhật: 15/03/2025

Bạn đã biết cách tính đạo hàm của ln ⁡x, nhưng còn cách tính nguyên hàm ln x thì sao? Đây là một chủ đề quan trọng trong giải tích, thường gặp trong các bài tập tích phân. Bài viết này Sforum sẽ phân tích chi tiết đạo hàm, nguyên hàm của ln x cùng với công thức và phương pháp tính.

Nguyên hàm là gì? Khái niệm nguyên hàm ln x

Nguyên hàm là một khái niệm quan trọng trong toán học, đặc biệt liên quan đến lĩnh vực tích phân. Một hàm F(x) được gọi là nguyên hàm của f(x) nếu F'(x) = f(x). Nói cách khác, nguyên hàm là phép toán ngược của phép đạo hàm.

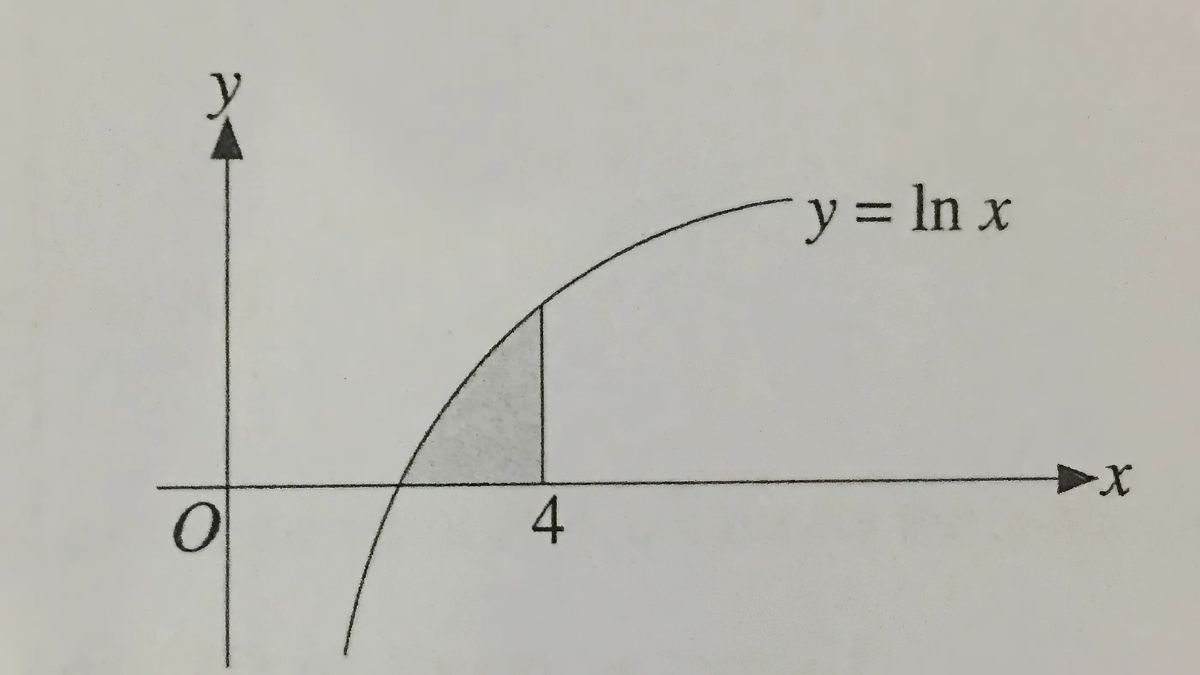
Khái niệm về nguyên hàm ln x và ln x đạo hàm

Trước khi đi sâu vào nguyên hàm ln x, chúng ta cần nhắc lại đạo hàm của hàm số logarit tự nhiên. Đạo hàm của ln x là 1/x. Điều này có nghĩa là nếu ta lấy đạo hàm của ln x, ta sẽ được 1/x. Vậy nguyên hàm của ln x là gì? Đó là hàm số F(x) mà khi ta lấy đạo hàm của F(x), ta sẽ thu được ln x.

Công thức và chứng minh công thức nguyên hàm của ln x

Công thức nguyên hàm của ln x được biểu diễn như sau:

∫ ln x dx = x(ln x - 1) + C

Trong đó:

∫: Ký hiệu của phép tính nguyên hàm.
C: Hằng số tích phân.

Công thức và chứng minh công thức nguyên hàm của ln x

Chứng minh: Để chứng minh công thức trên, ta có thể sử dụng phương pháp tích phân từng phần. Đặt:

u = ln x
dv = dx

Suy ra:

du = (1/x) dx
v = x

Áp dụng công thức từng phần, ta có:

∫ ln x dx = x ln x - ∫ x * (1/x) dx

= x ln x - ∫ dx

= x ln x - x + C

= x(ln x - 1) + C

Nếu việc học các khái niệm toán học như nguyên hàm ln x khiến bạn gặp khó khăn, thì việc sở hữu một chiếc laptop phù hợp có thể giúp bạn học tập hiệu quả hơn. Tại CellphoneS, các dòng laptop dành cho học sinh, sinh viên không chỉ đáp ứng nhu cầu học online mà còn hỗ trợ xử lý các phần mềm học thuật, giúp bạn dễ dàng tiếp cận và thực hành các bài toán từ cơ bản đến nâng cao. Tham khảo ngay!

[Product_Listing categoryid="1054" propertyid="" customlink="https://cellphones.com.vn/laptop/sinh-vien.html" title="Tham khảo danh sách laptop sinh viên được quan tâm tại CellphoneS!"]

Cách tính nguyên hàm ln x

Để giải quyết bài toán về cách tính nguyên hàm của ln⁡x, chúng ta cần hiểu rõ mối liên hệ giữa ln x đạo hàm và các phương pháp tính tích phân. Có hai cách tiếp cận phổ biến: sử dụng quy tắc tính nguyên hàm hoặc áp dụng phép tích phân từng phần.

Sử dụng quy tắc tính nguyên hàm

Để tính nguyên hàm ln x, ta trực tiếp áp dụng công thức đã chứng minh ở trên:

∫ ln x dx = x(ln x - 1) + C

Khi gặp các dạng bài toán yêu cầu tính nguyên hàm của ln⁡x, ta chỉ cần áp dụng trực tiếp công thức này để tìm ra kết quả. Đây là cách nhanh nhất để giải quyết các dạng bài tính cho ln x đạo hàm lẫn nguyên hàm đơn giản. Ví dụ:

∫ ln(2x)dx=xln(2x)−x+C

Sử dụng phép tích phân

Trong một số trường hợp phức tạp hơn, ta có thể sử dụng phép tích phân để tính nguyên hàm của ln x kết hợp với các kỹ thuật khác như đổi biến, từng phần. Phương pháp này dựa trên công thức:

Sử dụng phép tích phân

∫udv=uv−∫vdu

Trong trường hợp của ln⁡x, ta chọn:

u=lnx, khi đó du=(1/x)dx

dv=dx, khi đó v=x

Áp dụng công thức tích phân từng phần, ta có:

∫lnxdx=xlnx−∫x⋅(1/x)dx

Biểu thức bên trong tích phân rút gọn thành ∫1dx=x. Do đó:

∫lnxdx=xlnx−x+C

Các dạng bài tập nguyên hàm ln x

Bài toán về nguyên hàm ln x xuất hiện với nhiều biến thể, đòi hỏi sự linh hoạt trong cách tiếp cận và áp dụng công thức. Một số dạng phổ biến bao gồm hàm ln(x+1), tổ hợp 1+ln/x,... Ngoài ra, các dạng phức tạp hơn như ln(lnx)/x cũng yêu cầu kỹ năng tính toán cao và hiểu rõ phương pháp tích phân từng phần.

Dạng nguyên hàm ln(x+1)

Dạng bài tập này yêu cầu xác định nguyên hàm của các biểu thức chứa ln⁡(x+1). Phương pháp giải thường sử dụng tích phân từng phần, kết hợp với phép biến đổi biểu thức để đơn giản hóa. Đây là dạng bài tính nguyên hàm ln x phổ biến, thường xuất hiện trong các bài kiểm tra và đề thi, giúp rèn luyện kỹ năng, thao tác tính toán chính xác.

Ví dụ: Tính ∫ln(x+1)dx:

Ta sử dụng phương pháp từng phần, đặt:

Bài tập dạng nguyên hàm ln(x+1)

Áp dụng công thức: ∫udv=uv−∫vdu

Ta có:

Bài tập dạng nguyên hàm ln(x+1)

Do đó:

Bài tập dạng nguyên hàm ln(x+1)

Dạng nguyên hàm 1+ln/x

Dạng bài này có thể đơn giản hóa bằng cách chia từng số hạng trong ngoặc cho x. Dạng này kết hợp giữa một hằng số và biểu thức có ln/x, đòi hỏi bạn phải nắm vững quy tắc tách tích phân. Việc nhận diện cấu trúc của ln/x là chìa khóa để giải bài tập nhanh chóng và chính xác. Dạng bài này thường đi kèm với các phép biến đổi trung gian để tối ưu lời giải.