Lý thuyết phương trình đường thẳng và các bài tập vận dụng

Phương trình đường thẳng là kiến thức đặc biệt quan trọng trong chương trình Toán cấp 3. Việc hiểu rõ lý thuyết và biết cách áp dụng sẽ giúp bạn tự tin giải quyết các bài toán từ cơ bản đến nâng cao. Trong bài viết này, Sforum sẽ hướng dẫn bạn cách viết phương trình đường thẳng đi qua 2 điểm cùng những bài tập vận dụng chi tiết nhé!

Lý thuyết phương trình đường thẳng chi tiết nhất

Để hiểu rõ nguyên lý và cách giải quyết các bài tập về phương trình đường thẳng thì bạn cần nắm vững các lý thuyết nền tảng quan trọng. Cùng tìm hiểu một số kiến thức cơ bản mà Sforum đã tổng hợp được ngay sau đây để giúp bạn giải quyết dạng toán này nhé!

Vectơ chỉ phương của đường thẳng

Một vectơ được gọi là vectơ chỉ phương (VTCP) khi và chỉ khi giá của nó song song hoặc trùng với đường thẳng và đồng thời khác vectơ 0. Nó giúp xác định phương hướng của một đường thẳng và được vận dụng để giải quyết các bài toán hình học trong đó có cách viết phương trình đường thẳng.

Lưu ý:

• Có vô số VTCP cho đường thẳng ∆ bất kỳ.
• Một đường thẳng có VTCP là u thì bất kỳ vectơ nào có dạng ku (k ≠ 0) cũng là VTCP của đường thẳng đó.
• u ≠ 0.

Phương trình tham số của đường thẳng

Một đường thẳng có thể được biểu diễn thông qua phương trình tham số dưới dạng hệ phương trình 2 ẩn. Cho đường thẳng ∆ đi qua 2 điểm M₀(x₀;y₀) và nhận u(u₁,u₂) là VTCP thì phương trình tham số của ∆ được biểu diễn như sau:

Trong đó:

• t ∈ R
• Khi t thay đổi, ta sẽ thu được các tọa độ (x;y) khác nhau, đó là các điểm cùng nằm trên đường thẳng ∆.

Để tiện cho việc tra cứu và tìm hiểu những thông tin liên quan đến phương trình đường thẳng và những dạng toán khác bạn cần sắm một chiếc iPad xịn. Hãy ghé ngay CellphoneS hoặc tham khảo link dưới đây để khám phá những mẫu iPad chất lượng, chính hãng. Tìm hiểu ngay!

[Product_Listing categoryid="944" propertyid="" customlink="https://cellphones.com.vn/tablet/ipad.html" title="Các mẫu iPad đang được quan tâm nhiều tại CellphoneS"]

Vectơ pháp tuyến của đường thẳng

Vectơ pháp tuyến (VTPT) của đường thẳng là một vectơ có phương tạo góc 90 độ với đường thẳng đó và khác vectơ 0. VTPT thường được sử dụng để viết phương trình đường thẳng dạng tổng quát và nhiều bài toán hình học khác.

• Có vô số VTPT cho đường thẳng ∆ bất kỳ.
• Một đường thẳng có VTPT là u thì bất kỳ vectơ nào có dạng ku (k ≠ 0) cũng là VTPT của đường thẳng đó.
• n ≠ 0.

Phương trình tổng quát của đường thẳng

Đường thẳng ∆ đi qua 2 điểm M₀(x₀;y₀) và nhận n(a;b) là VTPT thì ∆ được biểu diễn dưới dạng phương trình tổng quát là:

a(x - x₀) + b(y - y₀) = 0 hay ax + by + c = 0 với c = -ax₀ - by₀

Trong đó:

• a,b,c ∈ R
• a² + b² ≠ 0

Các dạng đặc biệt:

• ∆: ax + c = 0, a ≠ 0 => ∆ song song với Oy hoặc trùng với Oy (a = 1 và c = 0).
• ∆: by + c = 0, b ≠ 0 => ∆ song song với Ox hoặc trùng với Ox (b = 1 và c = 0).
• ∆: ax + by = 0, a² + b² ≠ 0 => ∆ đi qua gốc tọa độ O(0; 0).

Vị trí tương đối của hai đường thẳng

Xét đường thẳng ∆₁ và ∆₂ lần lượt có phương trình là: ∆₁: a₁x + b₁y + c₁ = 0 và ∆₂: a₂x + b₂y + c₂ = 0. Giao điểm của hai đường này là nghiệm của phương trình sau:

Ta có 3 trường hợp sau:

• Hệ (1) vô số nghiệm => ∆₁ và ∆₂ trùng nhau.
• Hệ (1) có 1 nghiệm (x₀;y₀) => ∆₁ cắt ∆₂ tại điểm M(x₀;y₀).
• Hệ (1) vô nghiệm => ∆₁ // ∆₂.

Với a₂, b₂, c₂ ≠ 0, ta có cách xét vị trí tương đối của ∆₁ và ∆₂ như sau:

Góc giữa hai đường thẳng

Hai đường thẳng ∆₁ và ∆₂ lần lượt có phương trình là:

• ∆₁: a₁x + b₁y + c₁ = 0 với VTPT là n₁(a₁;b₁), a₁² + b₁² ≠ 0.
• ∆₂: a₂x + b₂y + c₂ = 0 với VTPT là n₂(a₂;b₂), a₂² + b₂² ≠ 0.

Góc tạo bởi ∆₁ và ∆₂ được ký hiệu là (∆₁,∆₂) = α nhỏ hơn hoặc bằng 90 độ. Khi đó, ta có công thức:

Lưu ý:

• ∆₁ ⊥ ∆₂ ⇔ n₁ ⊥ n₂ ⇔ a₁a₂ + b₁b₂ = 0.
• ∆₁ và ∆₂ lần lượt có phương trình đường thẳng là y = k₁x + m₁ và y = k₂x + m₂ thì ∆₁ ⊥ ∆₂ ⇔ k₁k₂ = -1.

Tính khoảng cách từ một điểm đến một đường thẳng

Khi xét khoảng cách từ một điểm tới một đường thẳng, ta xét độ dài đoạn thẳng vuông góc nối từ điểm đến đường thẳng đó. Trong trục tọa độ Oxy, với đường thẳng ∆: ax + by + c = 0 và điểm M(x₀,y₀) cho trước, ta có khoảng cách từ M đến ∆ được xác định theo công thức sau:

Bài tập vận dụng

Dạng 1: Cách viết phương trình đường thẳng đi qua 2 điểm

Hai điểm A(3;5) và B (1;4) cùng nằm trên đường thẳng d, hãy viết phương trình tổng quát của d.

Hướng dẫn giải:

Vì A, B thuộc d nên ta có AB là VTCP của ∆.

AB = (1 - 3;4 - 5) = (-2;-1) => vectơ pháp tuyến của ∆ là n(1;-2)

Chọn điểm A(3;5) thuộc đường thẳng ∆ ta có:

d: 1(x - 3) - 2(y - 5) = 0

⇔ x -3 - 2y + 10 = 0

⇔ x - 2y + 7 = 0.

Vậy phương trình đường thẳng d dạng tổng quát là d: x - 2y + 7 = 0.

Dạng 2: Xét vị trí của hai đường thẳng

Hãy xét vị trí tương đối của d₁, d₂ lần lượt có phương trình là:

1. d₁: 3x - 4y + 7 = 0, d₂: 6x - 8y - 5 = 0.
2. d₁: x + 2y + 8 = 0, d₂: 3x + 4y - 2 = 0.
3. d₁: 2x + 4y - 6 = 0, d₂: x + 2y - 3 = 0.

Hướng dẫn giải:

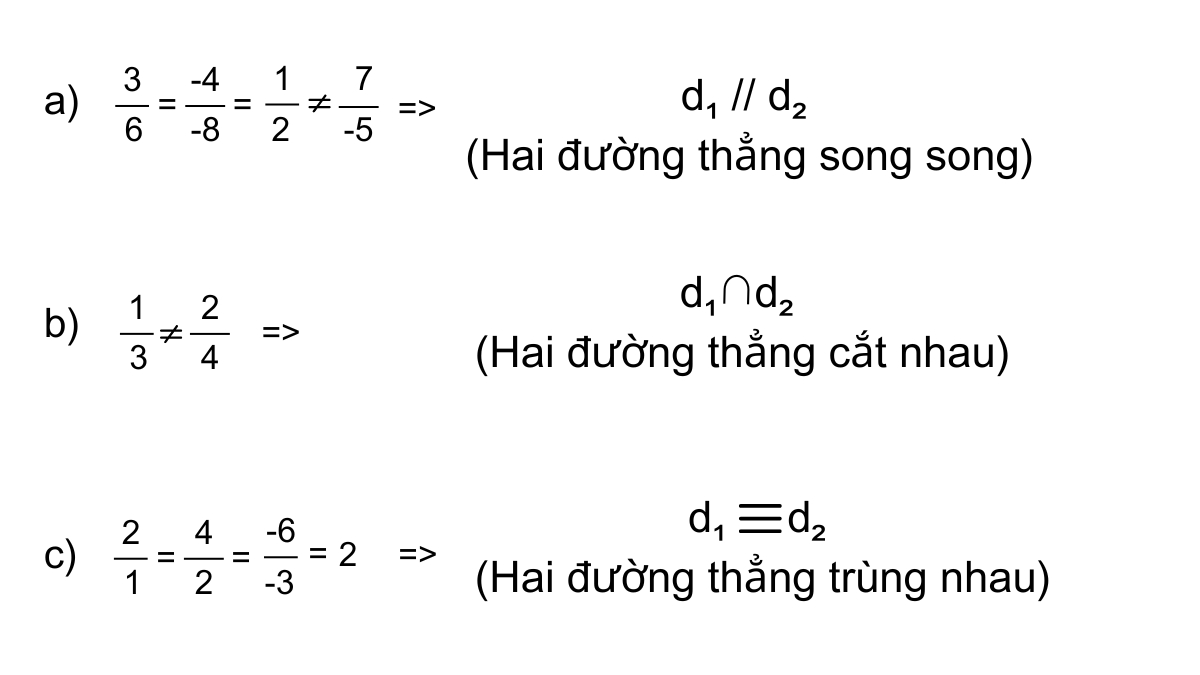
Dạng 3: Góc giữa 2 đường thẳng

Hãy xác định số đo góc giữa d và d’ biết hai đường này có phương trình tham số như sau:

Hướng dẫn giải:

Dạng 4: Khoảng cách từ điểm đến đường thẳng

Cho đường thẳng d: 2x + 3y - 29 = 0, hãy tính khoảng cách từ điểm A(3; 6) đến đường thẳng d.

Việc nắm vững các khái niệm vectơ, phương trình đường thẳng sẽ giúp bạn giải quyết tốt các bài tập từ cơ bản đến nâng cao. Sforum đã tổng hợp lý thuyết và những bài tập vận dụng trong bài viết trên. Hãy tìm hiểu và thường xuyên luyện tập cách viết phương trình đường thẳng đi qua 2 điểm để làm chủ dạng bài này nhé.

• Theo dõi thêm các kiến thức mới tại chuyên mục: Giáo dục; Góc Học & Day 4.0