Toàn bộ kiến thức về phương trình mặt phẳng bạn cần biết

Công thức, bài tập viết phương trình mặt phẳng là một chuyên đề toán thú vị được nhiều học sinh quan tâm. Nắm chắc khái niệm, các dạng bài tập của chuyên đề sẽ giúp học sinh tự tin hơn trong mỗi dịp thi cử. Nếu bạn chưa nắm được cách viết phương trình tổng quát của mặt phẳng Oxy thì đừng bỏ qua bài viết sau nhé! Toàn bộ kiến thức về chuyên đề này sẽ được chia sẻ chi tiết đến bạn.

Khái niệm về phương trình mặt phẳng

Để giải quyết được các dạng bài tập trong chuyên đề này, trước hết bạn cần nắm được: Vectơ chỉ phương, vectơ pháp tuyến, phương trình tổng quát của mặt phẳng là gì? Xem ngay những kiến thức sau để hiểu đúng về các khái niệm này nhé!

Vectơ chỉ phương và vectơ pháp tuyến của mặt phẳng

Vectơ chỉ phương của một mặt phẳng bất kì là các vectơ nằm trong (thuộc) hoặc có giá song song với mặt phẳng đó. Về số lượng, các vectơ chỉ phương của mỗi mặt phẳng là không giới hạn.

Vectơ pháp tuyến của một mặt phẳng là vectơ khác vectơ 0 và vuông góc với mặt phẳng đó. Giống như vectơ chỉ phương, số lượng vectơ pháp tuyến của mỗi mặt phẳng là vô số. Ngoài ra, trong cùng một mặt phẳng, các vectơ pháp tuyến có cùng phương với nhau. 

Phương trình tổng quát của mặt phẳng

Dưới đây là phương trình tổng quát của mặt phẳng trong không gian 3 chiều:

Ax + By + Cz + D = 0

Trong đó: 

• Vectơ pháp tuyến n = (A, B, C) với tổng các bình phương của A, B, C > 0.
• D là một hằng số xác định vị trí của mặt phẳng trong không gian.

Lưu ý: Công thức viết phương trình mặt phẳng tổng quát khi biết điểm thuộc và vectơ pháp tuyến của mặt phẳng đó.

iPad là công cụ hỗ trợ học tập hữu ích được nhiều bậc phụ huynh đầu tư. Không chỉ có thông tin về công thức phương trình mặt phẳng, có thể tìm kiếm thêm nhiều kiến thức, bài tập toán thú vị khác trên iPad. Nếu chưa biết mua iPad chính hãng, giá tốt tại đâu, bạn hãy ghé ngay CellphoneS để tham khảo nhé!

[Product_Listing categoryid="944" propertyid="" customlink="https://cellphones.com.vn/tablet/ipad.html" title="Các mẫu iPad đang được quan tâm nhiều tại CellphoneS"]

Vị trí tương đối giữa các mặt phẳng

Các mặt phẳng trong không gian 3 chiều có thể có các vị trí: song song, vuông góc, trùng nhau hoặc cắt nhau theo một đường thẳng.

Giả sử: Cho 2 mặt phẳng (A): Qx + My + Nz + D = 0 và (B): Q’x + M’y + N’z + D’ = 0. 

Trong đó: Q, M, N, D, Q’, M’, N’, D’ # 0.

Ta có:

• (A) và (B) cắt nhau khi: Q/Q’ # M/M’ # N/N’
• (A) và (B) trùng nhau khi: Q/Q’ = M/M’ = N/N’ = D/D’
• (A) và (B) song song khi: Q/Q’ = M/M’ = N/N’ # D/D’
• (A) và (B) vuông góc khi: QxQ’ + MxM’ + NxN’ = 0

 

Các dạng bài tập về phương trình mặt phẳng phổ biến

Nắm chắc công thức, các dạng bài tập phương trình mặt phẳng Oxy sẽ giúp bạn đạt được điểm cao trong các kì thi, kiểm tra. Dưới đây là những dạng bài tập hay gặp trong chuyên đề này, bạn hãy tham khảo với Sforum nhé!

Viết phương trình mặt phẳng đi qua 1 điểm có vectơ pháp tuyến cho trước

Bài tập: 

Biết mặt phẳng Oxy có vectơ pháp tuyến n = (4, 2, 5) và điểm M (2, 3, 1) thuộc mặt phẳng, yêu cầu viết phương trình mặt phẳng Oxy?

Lời giải: 

Dựa theo cách viết phương trình mặt phẳng có vectơ pháp tuyến cho trước và điểm nằm trong, ta có:

4(x - 2) + 2(y - 3) + 5(z - 1) = 0

Hay ta được phương trình rút gọn là:

4x + 2y + 5z – 19 = 0

Viết phương trình mặt phẳng đi qua 3 điểm không thẳng hàng

Bài tập: 

Hãy viết phương trình tổng quát của mặt phẳng (P) biết (P) đi qua 3 điểm A(2, 1, 4); B(4, 3, 5) và C(1, 5, 8).

Lời giải:

Bước 1: Xác định các vectơ AB và AC từ các điểm cho trước.

Vectơ AB = (4 – 2, 3 – 1, 5 – 4) = (2, 2, 1).

Vectơ AC = (1 – 2, 5 – 1, 8 – 4) = (-1, 4, 4).

Bước 2: Tìm Vectơ pháp tuyến của mặt phẳng (P).

Vectơ pháp tuyến = vectơ AB x Vectơ AC

Thay số ta được:

Vectơ pháp tuyến = (2x4-1x4, 1x(-1)-2x4, 2x4 – 2x(-1)) = (4, -9, 10).

Bước 3: Viết phương trình mặt phẳng (P) biết vectơ pháp tuyến và điểm đi qua.

(P): 4(x – 2) – 9(y – 1) + 10(z – 4) = 0

=> (P): 4x – 9y + 10z – 39 = 0

Phương trình mặt phẳng đi qua 1 điểm và song song với 1 mặt phẳng khác

Bài tập: 

Hãy viết phương trình mặt phẳng (Q) biết (Q) đi qua điểm Y (2, 5, 1) và (Q) // (P): 2x + 3y + 4z = 0.

Lời giải:

Mặt phẳng (P) có vectơ pháp tuyến n = (2, 3, 4). Vì (P) // (Q) nên n cũng là vectơ pháp tuyến của (Q).

Ta có mặt phẳng (Q) đi qua điểm Y (2, 5, 1) và có vectơ pháp tuyến n = (2, 3, 4). Vậy phương trình mặt phẳng (Q) là:

2(x – 2) + 3(y – 5) + 4(z – 1) = 0

Hay: 

2x + 3y + 4z – 23 = 0

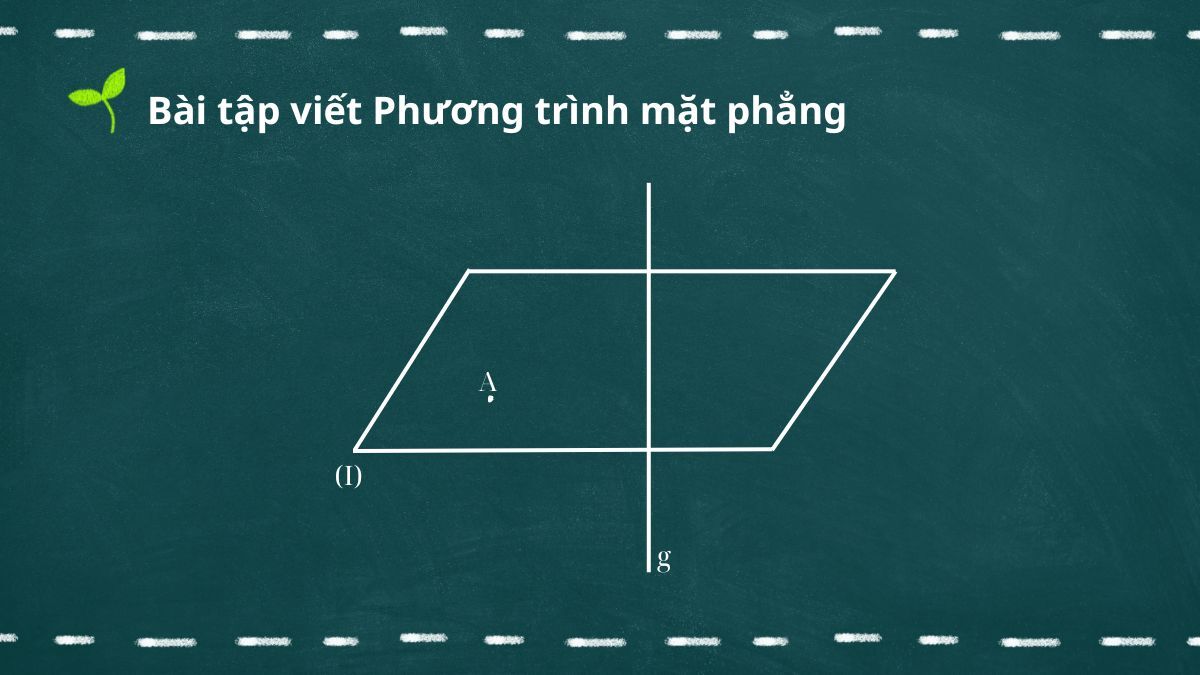
Phương trình mặt phẳng đi qua 1 điểm và vuông góc với 1 đường thẳng

Bài tập: 

Yêu cầu viết phương trình mặt phẳng (I) biết mặt phẳng (I) đi qua A (2, 3, 7) và (I) vuông góc với đường thẳng g: (x + 2)/1 = (y – 2)/(-1) = (z + 3)/2.

Lời giải:

Đường thẳng g có vectơ chỉ phương u = (1, -1, 2).

Vì mặt phẳng (I) vuông góc với đường thẳng g nên vectơ chỉ phương của g chính là vectơ pháp tuyến của (I).

Ta có phương trình của (I) khi biết (I) đi qua A (2, 3, 7) và có vectơ pháp tuyến n = (1, -1, 2) như sau:

1(x – 2) – 1(y – 3) + 2(z – 7) = 0

Hay:

x – y + 2z – 13 = 0

Viết phương trình mặt phẳng song song và cách đều 

Bài tập:

Cho phương trình 2 đường thẳng d, d’ có dạng như sau:

d: x = 2 + t; y = 1 – t; z = 2t.

d’: x + 2z – 2 = 0; y – 3 = 0.

Yêu cầu: Viết phương trình mặt phẳng (Q) song song và cách đều 2 đường thẳng d, d’.

Lời giải:

Ta có d có vectơ u chỉ phương = (1, -1, 2).

d’ có vectơ u’ chỉ phương = (-2, 0, 1).

Vì (Q) // d; (Q) // d’ => mặt phẳng Q có vectơ pháp tuyến n = (-1, -5, -2) (tích của hai vectơ chỉ phương của d và d’).

Vậy phương trình (Q) có dạng: -x – 5y – 2z + D = 0.

Lấy điểm A(2, 1, 0) thuộc d và điểm B(2, 3, 0) thuộc d’.

Theo đề bài khoảng cách từ mặt phẳng (Q) đến điểm A và B là như nhau nên:

• D = 12

Vậy phương trình của (Q) là: -x – 5y – 2z + 12 = 0.

Phương trình 2 mặt phẳng vuông góc với nhau

Bài tập:

Cho biết:

• Mặt phẳng (P) chứa đường thẳng h: x = -t, y = -1 + 2t, z = 2 + t
• Mặt phẳng (P) vuông góc mặt phẳng (Q): x + 2y – z + 1 = 0

Yêu cầu: Viết phương trình mặt phẳng (P).

Lời giải:

Ta có đường thẳng h đi qua điểm I(0, -1, 2) và có vectơ chỉ phương u = (-1, 2, 1).

Mặt phẳng (Q) có vectơ pháp tuyến n = (1, 2, -1).

Theo đề bài mặt phẳng (P) vuông góc với mặt phẳng (Q) và chứa đường thẳng h nên vectơ pháp tuyến n của (P) được tính như sau:

Vậy phương trình mặt phẳng (P) là:

-4(x – 0) – 4(z – 2) = 0

⬄ -4x – 4z + 8 = 0

⬄ x + z – 2 = 0

Trên đây là toàn bộ công thức, bài tập viết phương trình mặt phẳng hay gặp mà Sforum muốn chia sẻ đến bạn. Hi vọng bạn đã nắm được cách viết phương trình tổng quát của mặt phẳng Oxy cũng như các dạng bài tập liên quan. Đừng quên tại Sforum còn nhiều kiến thức, chuyên đề toán và giáo dục khác, bạn hãy tiếp tục dõi theo nhé!

Đọc thêm các bài viết cùng chủ đề: Góc Học & Dạy 4.0