Số phức là gì? Định nghĩa, ứng dụng và bài tập ví dụ

Bạn đã bao giờ tự hỏi công thức modun số phức là gì? Đây là nền tảng kiến thức không thể thiếu để giải quyết những bài toán phức tạp trong toán học hiện đại. Các vấn đề như cách chia số phức đối, liên hợp thường được đặt ra trong các bài toán và ứng dụng thực tế. Từ định nghĩa đến ứng dụng thực tế, các khái niệm này đều đóng vai trò nền tảng, đặc biệt khi làm việc với đại số và hình học trên mặt phẳng phức.

Định nghĩa của số phức

Số phức là một số được biểu thị dưới dạng sự kết hợp giữa một phần thực và một phần ảo. Nếu bạn thắc mắc tập hợp số phức ký hiệu là gì thì đó chính là 𝐶. Công thức như sau:

z=a+bi

Trong đó:

• a: phần thực của số phức
• b: phần ảo của số phức
• i: đơn vị ảo, với i² = -1

Ví dụ: 

• 3 + 2i, -5i, 7 đều là các số phức.
• 3 + 2i là một số phức, với phần thực là 3 và phần ảo là 4. 

Ngoài ra, số phức đối của z=a+bi là z=a-bi, được tạo ra bằng cách giữ nguyên phần thực và đổi dấu phần ảo. Còn 2 số phức và z=a+bi và z'=a'+b'i bằng nhau khi và chỉ khi phần thực a bằng a' và phần ảo b bằng b'.

Khi nhắc đến số phức là gì, ta thường nghĩ đến những khái niệm trừu tượng trong toán học. Nhưng cũng giống như cách số phức kết hợp giữa phần thực và phần ảo để giải quyết các bài toán phức tạp, một chiếc laptop phù hợp có thể trở thành công cụ hoàn hảo giúp học sinh, sinh viên cân bằng giữa học tập và giải trí. Tại CellphoneS, bạn sẽ tìm thấy những mẫu laptop sinh viên với giá cả hợp lý. Tham khảo ngay!

[Product_Listing categoryid="1054" propertyid="" customlink="https://cellphones.com.vn/laptop/sinh-vien.html" title="Tham khảo danh sách laptop sinh viên được quan tâm tại CellphoneS!"]

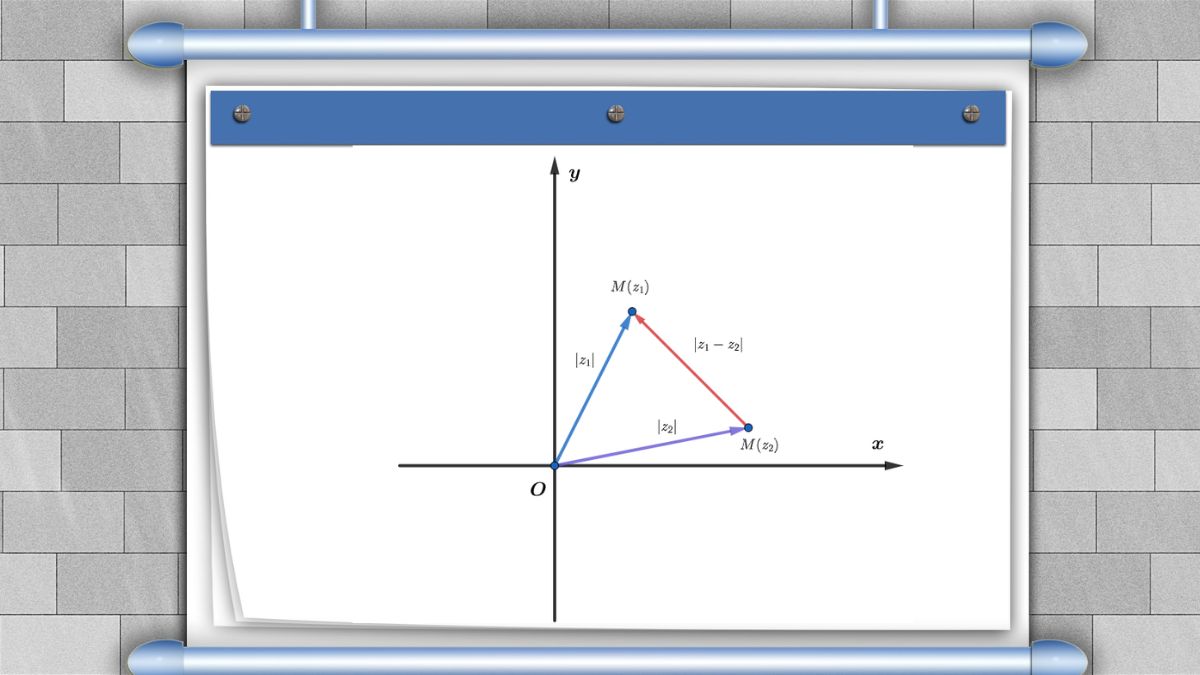
Biểu diễn dạng hình học của số phức

Số phức có thể được biểu diễn trên mặt phẳng phức (mặt phẳng Oxy). Trong đó:

• Trục hoành (Ox) biểu diễn phần thực (a).
• Trục tung (Oy) biểu diễn phần ảo (b).

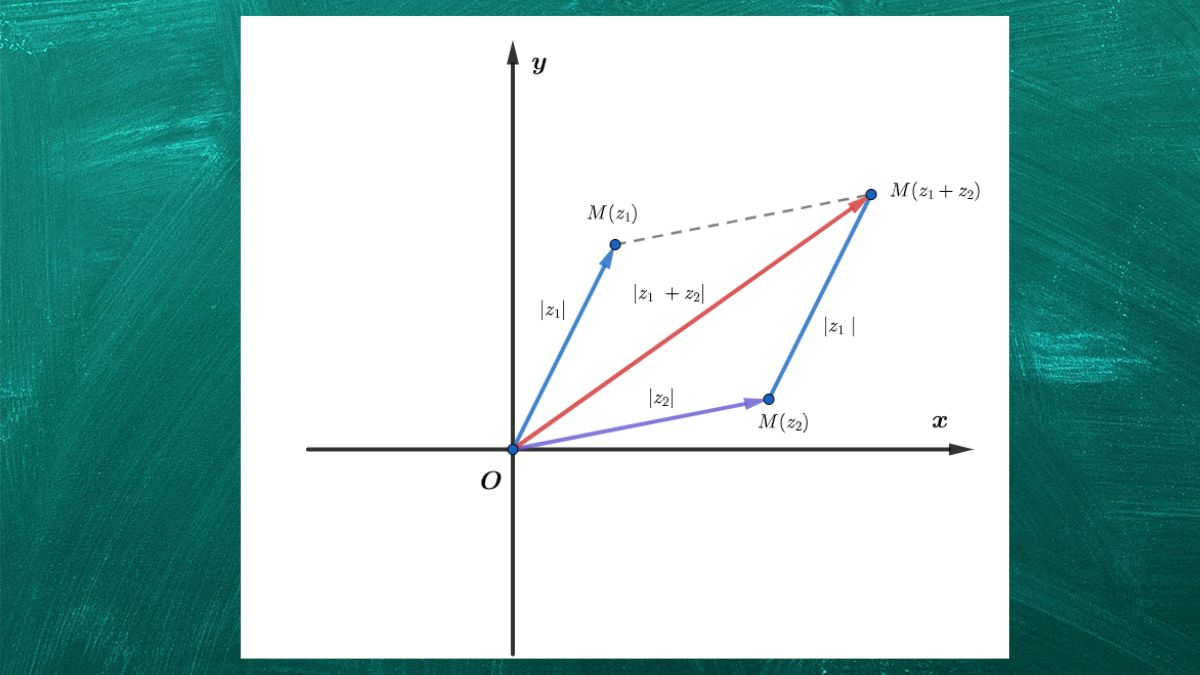
Mỗi số phức tương ứng với một điểm trên mặt phẳng này. Mỗi số phức z = a + bi khi đó sẽ được xác định một cách duy nhất bởi một điểm M(a, b) trên mặt phẳng. Điểm M này không chỉ đơn thuần là một điểm mà còn có thể được xem như một vectơ OM xuất phát từ gốc tọa độ O.

Một số khái niệm quan trọng về số phức

Khi nghiên cứu về số phức, ngoài khái niệm cơ bản, chúng ta còn gặp phải nhiều khái niệm quan trọng khác giúp mở rộng và làm rõ hơn các tính chất của nó. Những khái niệm này bao gồm số phức liên hợp, nghịch đảo, modun, argument,...

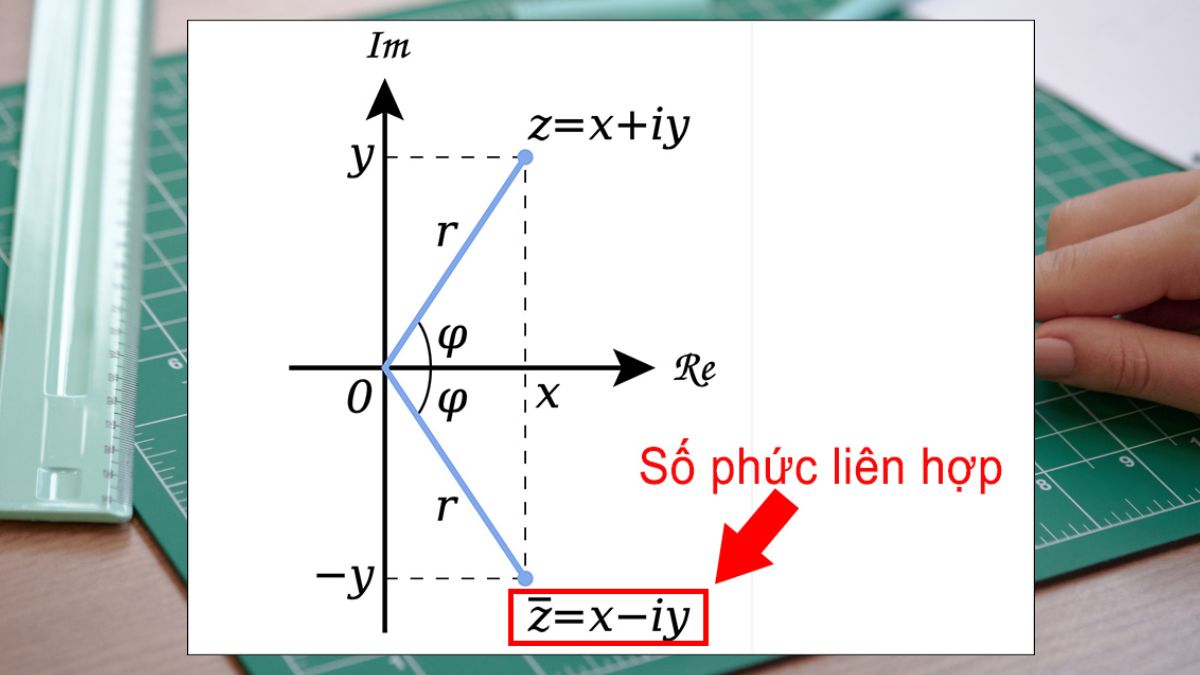
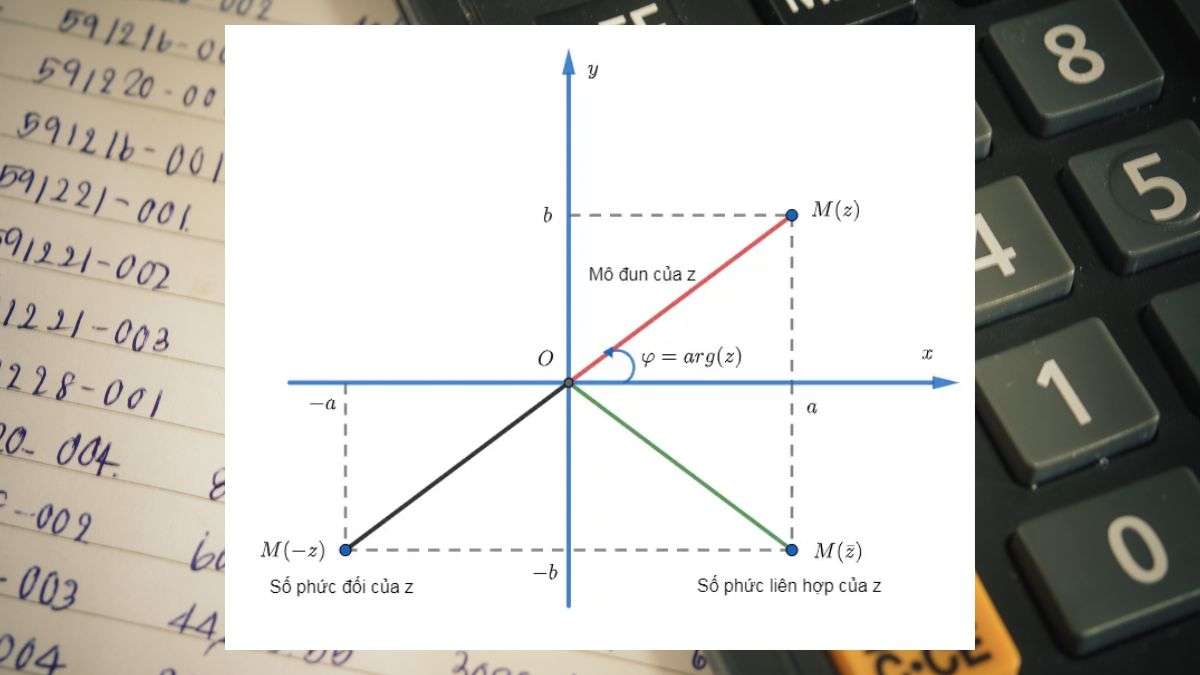
Số phức liên hợp

Số phức liên hợp của z = a + bi được tạo ra bằng cách giữ nguyên phần thực và đổi dấu phần ảo, là z' = a - bi. Về mặt hình học, đây là đối xứng của zzz qua trục hoành. Liên hợp của một số phức có nhiều ứng dụng quan trọng, đặc biệt trong việc tính toán modun, argument và thực hiện phép chia. Ngoài ra, số phức liên hợp còn được sử dụng rộng rãi trong các lĩnh vực như xử lý tín hiệu, lý thuyết điều khiển và cơ học lượng tử.

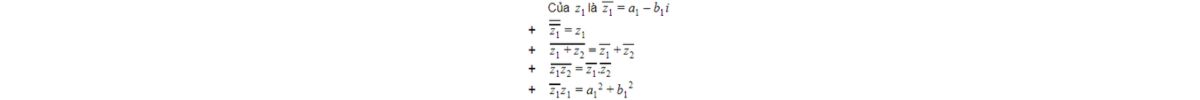
Số phức nghịch đảo

Số phức nghịch đảo của một số phức z ≠ 0, ký hiệu 1/z hoặc z-1, là một số phức w sao cho z.w = 1. Ta có thể chứng minh một cách chặt chẽ rằng 1/z = (a - bi) / (a² + b²) .

Khái niệm này có vai trò quan trọng trong phép chia và các phép biến đổi hình học liên quan đến nghịch đảo, được sử dụng rộng rãi trong các ứng dụng toán học và kỹ thuật. Công thức số phức nghịch đảo có thể được chứng minh như sau: 

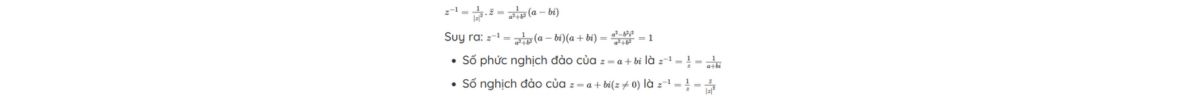
Modun của số phức

Modun của z = a + bi, ký hiệu |z|, là khoảng cách từ gốc tọa độ O đến điểm biểu diễn số phức z trên mặt phẳng phức. Modun |z| luôn là một số thực không âm và được tính bằng công thức |z| = √(a² + b²). Modun số phức cung cấp một cách đo "độ lớn" và có ý nghĩa hình học rõ ràng, được sử dụng thường xuyên trong nhiều bài toán liên quan đến các đại lượng phức hợp.

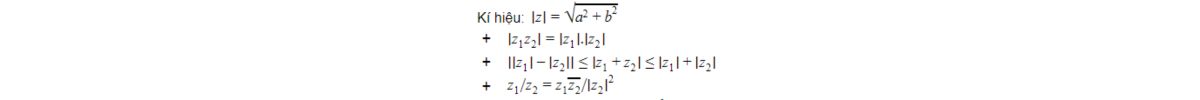
Argument của số phức

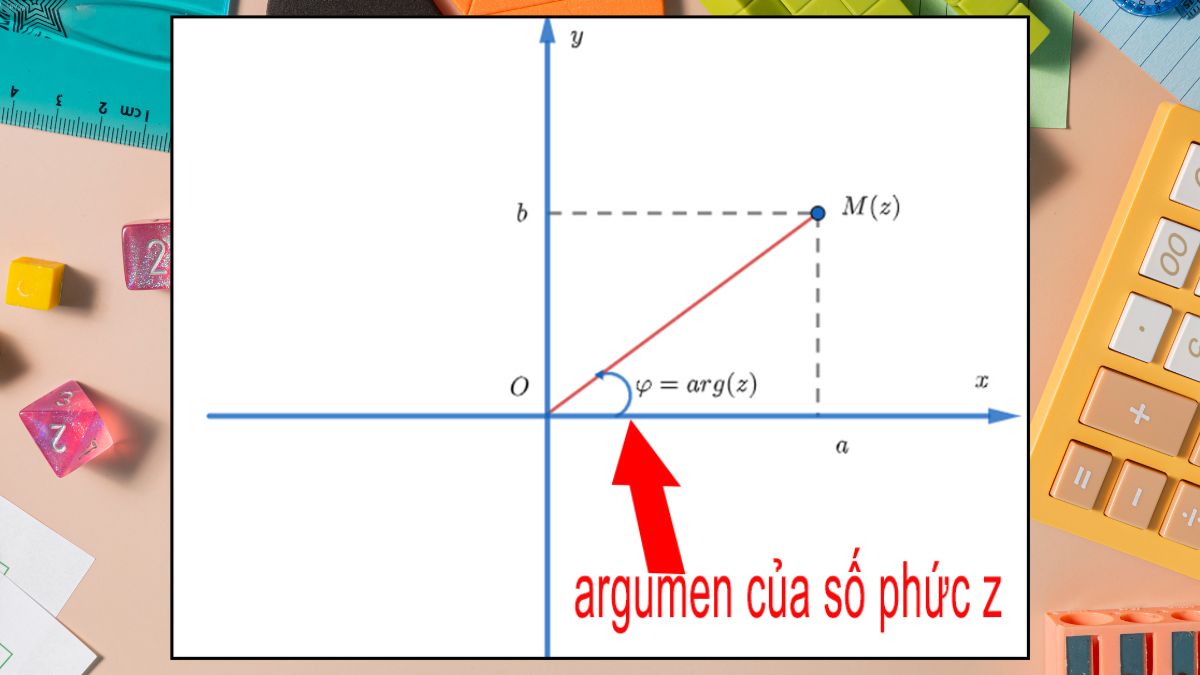
Argument của một số phức z ≠ 0, ký hiệu arg(z), là góc tạo bởi tia Ox dương và vectơ OM, trong đó M là điểm biểu diễn z trên mặt phẳng phức. Argument thường được đo bằng radian và có vô số giá trị, khác nhau bởi các bội số nguyên của 2π. Tuy nhiên, ta thường chọn giá trị chính của argument trong khoảng (-π, π]. 

Cụ thể hơn công thức số phức dạng lượng giác của z là: z = r(acosφ + isinφ). Trong đó, φ chính là một argument.

Dạng lượng giác của số phức

Mọi số phức z ≠ 0 đều có thể viết dưới dạng lượng giác: z = r(cosφ + isinφ). Trong đó r = |z| là modun của z và φ = arg(z) là argument của z.

Công thức số phức dạng lượng giác rất hữu ích trong các phép toán như nhân, chia, tìm căn bậc n, hoặc các bài toán liên quan đến mũ phức. Việc sử dụng dạng lượng giác không chỉ làm rõ bản chất hình học mà còn tối ưu hóa tính toán trong các bài toán kỹ thuật và ứng dụng thực tiễn.

Các phép toán trên số phức

Ngoài các phép cộng, trừ, và nhân, việc chia số phức cũng đóng vai trò quan trọng. Dưới đây là các công thức số phức giúp bạn thực hiện những phép toán này một cách chính xác.

Cộng, trừ: Thực hiện tương tự như phép cộng, trừ đa thức:

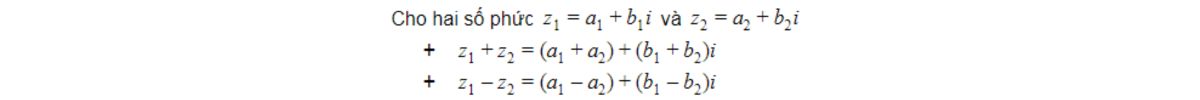
Nhân: Áp dụng quy tắc phân phối và sử dụng i² = -1.

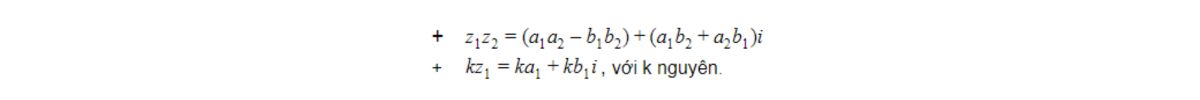
Chia: Cách chia số phức bằng phương pháp nhân cả tử và mẫu với số phức liên hợp của mẫu.

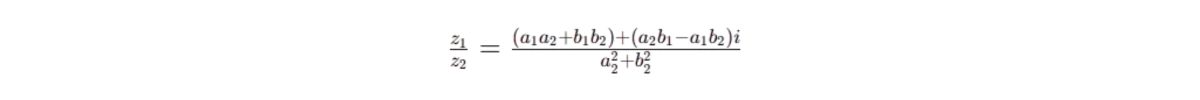
Một số bài tập về số phức

Bài tập 1: Tính modun và argument của z=1+i

Lời giải:

• Tính modun:
  Modun của một số phức z=a+bi được tính theo công thức:

 

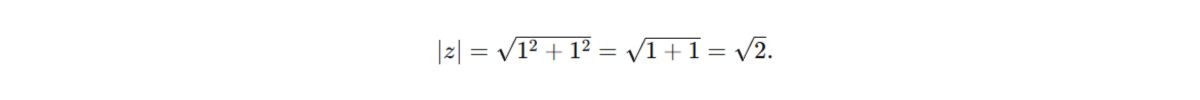
• Tính argument:
  Argument số phức là góc θ mà vector số phức tạo với trục thực, được tính bằng:

Bài tập 2: Tìm tổng, hiệu, tích và thương của hai số phức z1=2+3i và z2=1−i

Lời giải:

• Tổng: z1+z2 =(2+1)+(3−1)i=3+2i
• Hiệu: z1−z2=(2−1)+(3−(−1))i=1+4i
• Tích: z1⋅z2=(2⋅1−3⋅(−1))+(2⋅(−1)+3⋅1)i=(2+3)+(−2+3)i=5+i
• Thương: Áp dụng cách chia số phức như sau:

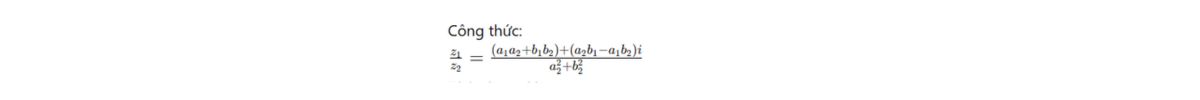
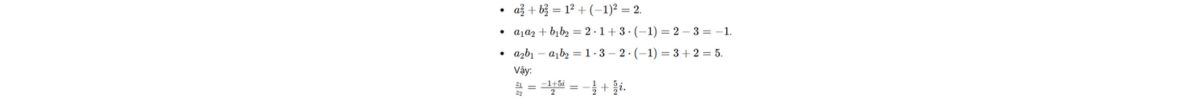
Bài tập 3: Viết số phức sau dưới dạng lượng giác:

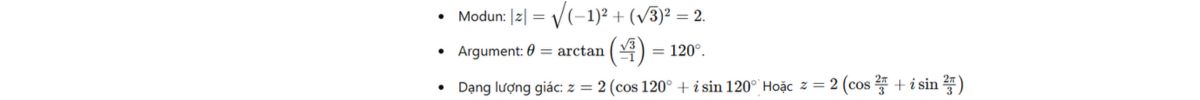
Việc hiểu rõ công thức modun số phức là gì và áp dụng chúng cùng với các khái niệm như cách chia số phức đối, liên hợp sẽ giúp bạn giải quyết hiệu quả các bài toán phức tạp. Dù bạn mới bắt đầu hay đang nâng cao kỹ năng, việc nắm chắc kiến thức này là chìa khóa để thành công trong các lĩnh vực liên quan đến toán học, giáo dục và kỹ thuật.

Xem thêm các bài viết cùng chủ đề: Góc Học & Dạy 4.0