Công thức tính thể tích hình trụ: Cách tính nhanh, chính xác

Công thức tính thể tích hình trụ tròn là những kiến thức quan trọng trong toán học, không chỉ xuất hiện thường xuyên trong bài tập mà còn có ứng dụng thực tế rộng rãi. Đặc biêt, công thức tính thể tích của hình trụ là kiến thức quan trọng để giải quyết các bài toán về hình học không gian. Bài viết dưới đây sẽ cung cấp đầy đủ kiến thức và hướng dẫn chi tiết để bạn làm chủ chủ đề này một cách dễ dàng và hiệu quả.

Tổng hợp công thức tính hình trụ chi tiết

Hình trụ là một khối hình học quen thuộc và cơ bản trong không gian. Dưới đây, Sforum sẽ hướng dẫn chi tiết thể tích hình trụ công thức, cách tính diện tích xung quanh và toàn phần, giúp bạn hiểu và áp dụng trong học tập cũng như thực tế.

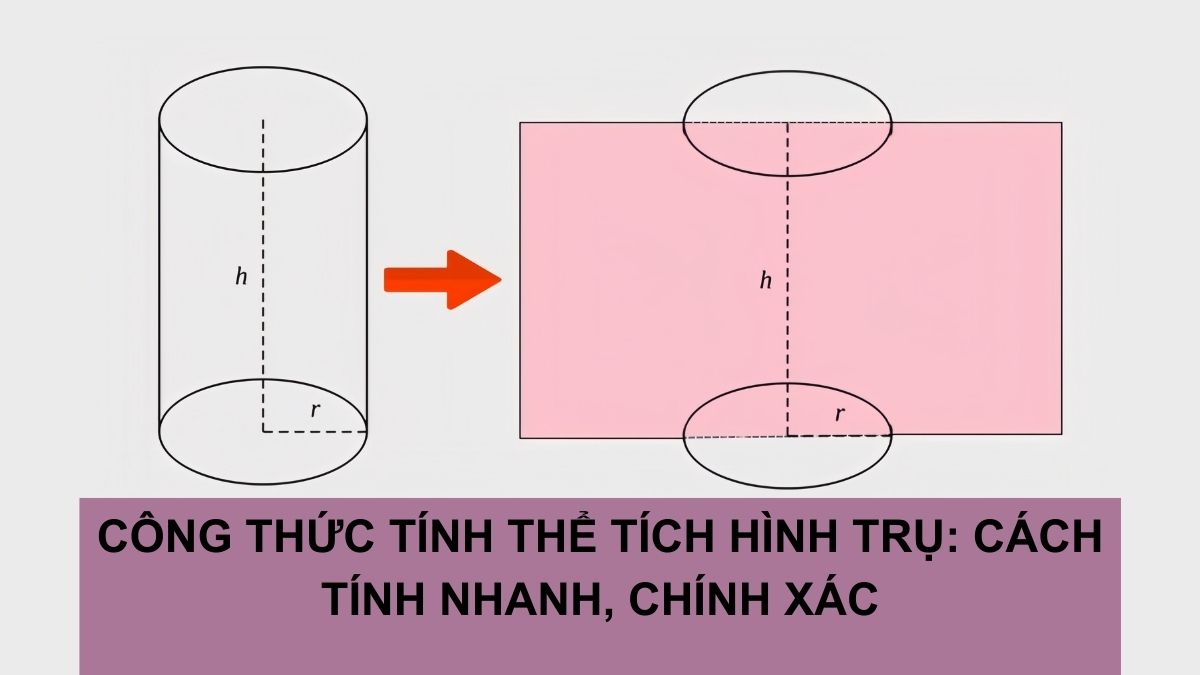
Công thức tính thể tích hình trụ

Thể tích hình trụ là một đại lượng biểu thị không gian mà hình trụ chiếm giữ, được xác định dựa trên diện tích đáy và chiều cao của hình. Thể tích được xác định dựa trên diện tích đáy và chiều cao. Công thức như sau:
V = πr²h

• V: Thể tích hình trụ.
• r: Bán kính đáy.
• h: Chiều cao.

Bằng cách sử dụng công thức tính thể tích của hình trụ, bạn có thể dễ dàng tính toán chính xác nếu xác định đúng các thông số.

Tìm hiểu về hình trụ dễ dàng hơn với một chiếc điện thoại từ CellphoneS. Các mẫu điện thoại giá ưu đãi dành cho học sinh, sinh viên giúp bạn học tập mọi lúc, mọi nơi. CellphoneS là lựa chọn hoàn hảo hỗ trợ việc học của bạn!

[Product_Listing categoryid="3" propertyid="" customlink="https://cellphones.com.vn/mobile.html" title="Danh sách điện thoại đang được quan tâm nhiều tại CellphoneS"]

Diện tích xung quanh hình trụ

Diện tích xung quanh của hình trụ là diện tích của toàn bộ mặt bên, không tính phần diện tích của hai đáy. Đây là một đại lượng thường được sử dụng trong các bài toán tính toán về bề mặt hoặc ứng dụng thực tế. Chẳng hạn như xác định lượng vật liệu cần thiết để phủ kín mặt bên của một bồn chứa hay ống dẫn.

Công thức tính diện tích xung quanh hình trụ như sau:

Sxq=2πrh

Trong đó:

• Sxq: Diện tích xung quanh.
• r: Bán kính đáy.
• h: Chiều cao.

Diện tích toàn phần hình trụ

Diện tích toàn phần của hình trụ là tổng diện tích bề mặt, bao gồm cả diện tích xung quanh và diện tích hai đáy. Đây là một đại lượng quan trọng trong hình học và có nhiều ứng dụng thực tế. Với công thức tính thể tích hình trụ, bạn có thể dễ dàng tính toán diện tích toàn phần, giúp xác định chính xác lượng vật liệu cần dùng khi sơn, dán toàn bộ bề mặt.

Công thức tính diện tích toàn phần của hình trụ như sau:

Stp= Sxq+ 2πr2= 2πrh + 2πr2

Trong đó: 

• Stp: Diện tích toàn phần hình trụ.
• Sxq: Diện tích xung quanh.
• r: Bán kính đáy.
• h: Chiều cao.

Hướng dẫn cách xác định các giá trị khi tính thể tích hình trụ

Khi tính thể tích hình trụ, việc xác định chính xác các giá trị như bán kính đáy, diện tích đáy tròn và chiều cao là cực kỳ quan trọng. Những giá trị này sẽ hỗ trợ bạn áp dụng chính xác công thức tính thể tích hình trụ và thực hiện các phép tính một cách chuẩn xác. Dưới đây là các bước hướng dẫn chi tiết giúp bạn xác định các giá trị này.

Xác định bán kính đáy hình trụ

Xác định bán kính đáy hình trụ là một bước quan trọng khi áp dụng công thức tính thể tích hình trụ tròn. Bán kính đáy (ký hiệu là r) chính là khoảng cách từ tâm của đáy tròn đến bất kỳ điểm nào trên vòng tròn đó. Để tính bán kính đáy, bạn có thể đo trực tiếp hoặc tính từ chu vi của đáy.

Công thức tính bán kính từ chu vi đáy là: r =C2π

Trong đó: C là chu vi của đáy, có thể đo được nếu biết chiều dài vòng tròn bao quanh đáy hình trụ.

Xác định diện tích đáy tròn

Xác định diện tích đáy tròn của hình trụ là một bước quan trọng trong quá trình tính thể tích. Bởi vì đáy của hình trụ có dạng hình tròn, nên diện tích của đáy chính là diện tích của một hình tròn có bán kính r.

Công thức tính diện tích đáy hình trụ được đưa ra như sau:

A = πr²

Trong đó:

• A là diện tích của đáy hình trụ.
• r là bán kính của đáy.

Xác định chiều cao hình trụ

Xác định chiều cao hình trụ là bước quan trọng khi tính thể tích. Chiều cao là khoảng cách vuông góc giữa hai đáy, tức đoạn thẳng nối từ đáy dưới lên đáy trên theo phương thẳng đứng. Để xác định chiều cao, bạn có thể:

• Đo trực tiếp: Nếu có mô hình hình trụ, dùng thước đo khoảng cách giữa hai đáy.
• Dựa vào thông số bài toán: Trong nhiều bài toán, chiều cao đã được cung cấp sẵn.
• Tính toán: Nếu chỉ có bán kính đáy và các yếu tố khác, bạn có thể sử dụng công thức thể tích để tính chiều cao.

Lưu ý cần tránh khi tính thể tích hình trụ

Khi tính thể tích hình trụ, dù công thức tính toán có vẻ đơn giản, nhưng nếu áp dụng sai các thông số hoặc giá trị liên quan, bạn có thể nhận được kết quả không chính xác. Để đảm bảo tính toán đúng theo thể tích hình trụ công thức, dưới đây là những lưu ý quan trọng bạn cần tránh.

Nhầm giữa chiều cao (h) và bán kính đáy (r)

Trong công thức tính thể tích hình trụ tròn, mỗi thông số có vai trò rất quan trọng và không thể thay thế cho nhau. Bán kính đáy (r) là độ dài từ tâm của đáy tròn đến mép ngoài của nó. Chiều cao (h) là khoảng cách thẳng đứng giữa hai đáy của hình trụ. Nhầm lẫn giữa bán kính và chiều cao có thể khiến bạn tính sai thể tích, dẫn đến kết quả hoàn toàn sai lệch. Do đó, khi giải bài toán, bạn cần kiểm tra kỹ lưỡng và phân biệt rõ ràng các thông số này.

Không tính chính xác giá trị của số pi (π)

Số pi (π) là một hằng số không có giá trị chính xác, nhưng trong toán học, chúng ta thường làm tròn π về giá trị 3.14 hoặc 227 trong những phép tính đơn giản. Tuy nhiên, trong một số bài toán yêu cầu độ chính xác cao, việc làm tròn quá mức hoặc không chính xác sẽ dẫn đến sai sót trong kết quả cuối cùng. 

Để đảm bảo kết quả chính xác nhất, bạn nên sử dụng giá trị π càng gần chính xác càng tốt, hoặc sử dụng máy tính hoặc phần mềm tính toán để tự động tính giá trị π với độ chính xác cao. 

Tips tính thể tích hình trụ chính xác

Để đạt được kết quả chính xác và nhanh chóng khi tính thể tích hình trụ, việc áp dụng các mẹo sau đây là rất cần thiết. Những gợi ý này không chỉ giúp bạn tiết kiệm thời gian mà còn giảm thiểu khả năng mắc phải sai sót trong quá trình tính toán.

Sử dụng máy tính

Máy tính cầm tay hoặc phần mềm hỗ trợ tính toán có thể là công cụ vô cùng hữu ích khi bạn cần tính thể tích hình trụ chính xác. Đặc biệt trong các bài toán phức tạp, việc áp dụng thể tích hình trụ công thức bằng phương pháp tính tay có thể dẫn đến sai sót do quá trình làm tròn số hoặc thao tác tính toán. 

Với phần mềm hoặc máy tính, bạn chỉ cần cài đặt độ chính xác của kết quả, và máy sẽ tự động xử lý quá trình làm tròn mà không có bất kỳ sai sót nào. Điều này vừa giúp rút ngắn thời gian vừa đảm bảo độ chính xác cho kết quả.

Làm tròn kết quả hợp lý (Theo yêu cầu nếu có)

Trong nhiều bài toán toán học, yêu cầu làm tròn kết quả là một phần quan trọng không thể thiếu. Tuy nhiên, khi áp dụng công thức tính thể tích hình trụ tròn hoặc các bài toán khác, điều quan trọng là bạn phải làm tròn kết quả một cách hợp lý và đúng theo yêu cầu của đề bài. Nếu đề bài yêu cầu làm tròn đến một hoặc hai chữ số thập phân, hãy chắc chắn thực hiện đúng để tránh mất điểm trong kỳ thi hoặc bài kiểm tra.

Việc làm tròn kết quả không chỉ giúp bạn đưa ra đáp án chính xác mà còn làm cho bài làm của bạn trở nên rõ ràng và dễ hiểu hơn. Khi không có yêu cầu cụ thể về số chữ số thập phân, hãy làm tròn sao cho kết quả vẫn dễ hiểu và có thể sử dụng hiệu quả trong các bước tính toán tiếp theo.

Lựa chọn đơn vị đo phù hợp

Một sai lầm thường gặp khi tính thể tích hình trụ là không đảm bảo sự đồng nhất giữa các đơn vị đo. Đảm bảo rằng tất cả các thông số như bán kính đáy (r), chiều cao (h) và kết quả thể tích (V) được đo bằng cùng một đơn vị. 

Nếu bán kính và chiều cao được đo bằng centimet, thể tích sẽ được tính bằng centimet khối (cm³). Nếu các thông số có đơn vị khác nhau (chẳng hạn bán kính tính bằng mét và chiều cao tính bằng centimet), bạn cần đổi nó về cùng một đơn vị trước khi tính toán. Việc này rất quan trọng vì sự không đồng nhất về đơn vị có thể dẫn đến kết quả sai lệch và ảnh hưởng đến tính chính xác của bài toán.

Giải bài tập kèm lời giải chi tiết về thể tích hình trụ

Bài tập 1: Một hình trụ có bán kính đáy r = 5 cm và chiều cao h = 10 cm. Hãy tính thể tích của hình trụ.

Lời giải:
Áp dụng công thức:
V = π × r² × h = 3.14 × 5² × 10 = 785 cm³.

Vậy thể tích hình trụ là 785 cm³.

Bài tập 2: Một hình trụ có thể tích V = 1570 cm³ và bán kính r = 7 cm. Hãy tính chiều cao h.

Lời giải:
Áp dụng công thức:
h = Vπ × r² = 15703.14 × 7² ≈ 10 cm.

Đáp án chiều cao của hình trụ là 10 cm.

Bài tập 3: Một hình trụ có bán kính đáy r = 3 cm và chiều cao h = 8 cm. Hãy tính diện tích xung quanh của hình trụ.

Lời giải:
Áp dụng công thức tính diện tích xung quanh hình trụ:
Sxq=2πrh= 23,1483 =150.72cm2

Kết luận: Diện tích xung quanh của hình trụ là 150.72 cm².

Bài tập 4: Một hình trụ có diện tích đáy là 78.5 cm² và chiều cao h = 10 cm. Hãy tính thể tích của hình trụ.

Lời giải:
Biết diện tích đáy của hình trụ là A = πr², từ đó ta có thể tính bán kính đáy r.
A= 78.5 =3.14×r² => r= 78.53.14=25 = 5cm

Sau khi xác định bán kính, ta có thể tính thể tích của hình trụ:
V = π × r² × h = 3.14 × 52 ×10= 3.14 × 25 × 10 = 785cm³

Kết luận: Thể tích của hình trụ là 785 cm³.

Công thức tính thể tích hình trụ tròn và các ứng dụng liên quan là phần kiến thức quan trọng trong toán học và thực tiễn. Hiểu rõ công thức tính thể tích của hình trụ, cách xác định các giá trị và tránh những sai lầm thường gặp sẽ giúp bạn giải quyết bài toán một cách dễ dàng. Hy vọng bài viết đã cung cấp những thông tin hữu ích giúp bạn hiểu và áp dụng một cách hiệu quả. Hãy lưu lại để tham khảo khi cần thiết!