Đường phân giác là gì? Tính chất và ví dụ minh họa

Trong hình học, việc xác định chân đường phân giác là gì là một kiến thức quan trọng giúp giải quyết nhiều bài toán về tam giác. Bên cạnh đó, một câu hỏi thường gặp là giao điểm của 3 đường phân giác là gì và nó có vai trò gì trong hình học. Hiểu rõ các khái niệm này sẽ giúp bạn dễ dàng áp dụng vào thực tế cũng như trong các bài toán chứng minh hình học.

Định nghĩa đường phân giác là gì

Một tia được gọi là đường phân giác của góc khi nó nằm bên trong góc đó và chia góc thành hai phần có số đo bằng nhau. Khi vẽ ba đường phân giác của một tam giác, chúng luôn cắt nhau tại một điểm duy nhất trong tam giác đó. Giao điểm của ba đường phân giác chính là tâm của đường tròn nội tiếp tam giác, thường được gọi là tâm nội tiếp.

Trong thực tế, đường phân giác thường được sử dụng để tìm mối quan hệ về độ dài các đoạn thẳng trong tam giác, xác định tâm đường tròn nội tiếp và giải quyết nhiều bài toán hình học quan trọng.

Laptop là công cụ hỗ trợ đắc lực trong việc tìm hiểu đường phân giác, giúp bạn tra cứu tài liệu và xem bài giảng một cách thuận tiện. Với màn hình sắc nét và hiệu năng ổn định, bạn có thể dễ dàng vẽ hình, thực hành bài tập trực quan hơn. Tìm hiểu ngay để chọn laptop giúp bạn học tập hiệu quả hơn !

[Product_Listing categoryid="380" propertyid="" customlink="https://cellphones.com.vn/laptop.html" title="Danh sách Laptop đang được quan tâm nhiều tại CellphoneS"]

Tính chất của đường phân giác 

Nắm vững tính chất đường phân giác giúp bạn dễ dàng giải quyết nhiều bài toán liên quan đến tam giác và các góc trong hình học. Những tính chất đường phân giác này không chỉ giúp giải quyết bài toán hình học mà còn là nền tảng quan trọng trong việc chứng minh các mối quan hệ hình học phức tạp hơn.

• Định lý đường phân giác: một góc trong tam giác khi được chia bởi đường phân giác sẽ tạo ra hai đoạn trên cạnh đối diện có tỉ lệ bằng tỉ số hai cạnh kề của góc đó.

 

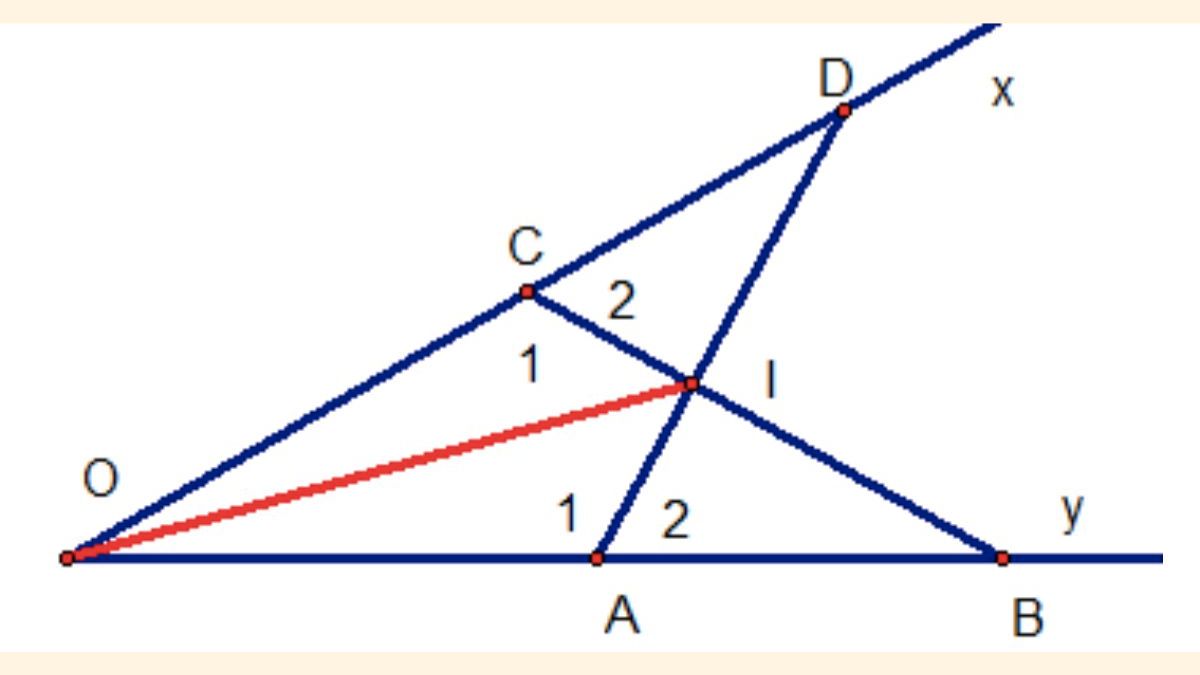
• Ba đường phân giác đồng quy tại một điểm: Khi ba đường phân giác của một tam giác cắt nhau tại một điểm, điểm này chính là tâm của đường tròn nội tiếp, đóng vai trò quan trọng trong các bài toán về đối xứng và hình tròn.
• Đối với tam giác cân, đường phân giác không chỉ chia góc thành hai phần bằng nhau mà còn đóng vai trò là đường trung tuyến và đường cao, giúp tạo ra hai tam giác nhỏ đồng dạng.

Hướng dẫn cách vẽ đường phân giác 

Việc biết cách vẽ đường phân giác chính xác giúp bạn áp dụng hiệu quả vào bài tập. Một trong những phương pháp phổ biến là sử dụng thước đo góc để xác định đường phân giác một cách dễ dàng.

Bước 1: Đầu tiên, đặt thước đo góc sao cho điểm giữa của thước nằm đúng tại đỉnh góc cần chia. 

Bước 2: Đọc số đo của góc, chia đôi giá trị này để xác định điểm nằm giữa hai tia của góc. Đánh dấu điểm này trên cung tròn để làm cơ sở vẽ đường phân giác.

Bước 3: Nối đỉnh góc với điểm vừa đánh dấu để tạo thành tia phân giác. Sau đó, thêm ký hiệu vào hình để thể hiện rằng hai góc được chia có số đo bằng nhau.

Các ví dụ minh họa 

Bài toán về đường phân giác thường được chia thành hai nhóm chính: chứng minh một tia là đường phân giác của một góc và tính số đo góc dựa vào tính chất đường phân giác. Dưới đây là một số bài toán minh họa giúp bạn áp dụng kiến thức này một cách hiệu quả.

• Ví dụ 1: Chứng minh một tia là đường phân giác

Cho tam giác ABC, biết rằng tia AD nằm bên trong góc BAC và thỏa mãn điều kiện góc BAD bằng góc CAD. Hãy xác định xem AD có chia góc BAC thành hai phần bằng nhau hay không để chứng minh đó là đường phân giác.

Lời giải: Theo định nghĩa, nếu một tia chia một góc thành hai góc bằng nhau, thì tia đó là đường phân giác. Vì góc BAD = góc CAD theo giả thiết, suy ra AD chính là đường phân giác của góc BAC.

• Ví dụ 2: Tính số đo góc khi biết đường phân giác

Cho góc xOy có số đo 70°. Tia Oz là đường phân giác của góc xOy. Tính số đo của góc xOz.

Lời giải: Theo tính chất đường phân giác, khi một góc được chia thành hai phần bằng nhau, mỗi phần có số đo bằng một nửa góc ban đầu. Do đó, góc xOz = 70° : 2 = 35°.

Việc nắm vững khái niệm chân đường phân giác là gì giúp bạn áp dụng vào các bài toán về hình học tam giác. Ngoài ra, nắm được giao điểm của 3 đường phân giác là gì còn hỗ trợ trong việc xác định tâm đường tròn nội tiếp và các ứng dụng liên quan. Hy vọng bài viết này giúp bạn củng cố kiến thức và vận dụng thành thạo vào các bài toán hình học. Nếu muốn cập nhật thường xuyên các thông tin, kiến thức đề tài giáo dục thì bạn hãy truy cập Sforum hàng ngày để có thông tin mới nhất nhé!

Đọc các bài viết cùng chuyên mục: Góc Học & Dạy 4.0