Lý thuyết & Dấu hiệu nhận biết hai đường thẳng song song

Bạn đã nắm vững tính chất, dấu hiệu nhận biết và cách chứng minh hai đường thẳng song song hay chưa? Đây là kiến thức khá quan trọng trong hình học, giúp bạn dễ dàng nhận diện và áp dụng vào bài toán thực tế. Hãy đọc bài viết sau của Sforum để hiểu hơn về hai đường thẳng đặc biệt này nhé!
Lý thuyết về hai đường thẳng song song
Trong mặt phẳng, 2 đường thẳng có vị trí là song song khi và chỉ khi giữa chúng không tồn tại bất kỳ điểm chung nào. Nói cách khác, nếu đường thẳng Δ cắt hai đường thẳng bất kỳ và tạo ra cặp góc so le (hoặc góc đồng vị) có số đo bằng nhau thì ta có thể kết luận chúng song song. Đây là một trong những dấu hiệu quan trọng giúp nhận biết quan hệ song song giữa hai đường thẳng. Ký hiệu song song được viết là: a//b.

Hãy sắm ngay một chiếc iPad chính hãng tại CellphoneS với màn hình trực quan để có thể tiếp cận với việc học toán hình một cách đơn giản hơn. Cửa hàng hiện đang có rất nhiều sản phẩm iPad giá tốt đến từ nhiều thương hiệu nổi tiếng. Nếu bạn có nhu cầu, hãy xem danh sách sản phẩm ở link dưới đây. Tìm hiểu thêm!
[Product_Listing categoryid="944" propertyid="" customlink="https://cellphones.com.vn/tablet/ipad.html" title="Các mẫu iPad đang được quan tâm nhiều tại CellphoneS"]
Dấu hiệu nhận biết hai đường thẳng song song
Trong mặt phẳng, 2 đường thẳng không tồn tại bất kỳ điểm chung nào thì song song. Để xác định tính chất này, ta có thể dựa vào các dấu hiệu nhận biết thông qua góc tạo bởi một đường thẳng cắt chúng.

Nếu xảy ra một trong các trường hợp sau, bạn có thể kết luận rằng hai đường thẳng song song:
- Số đo 1 cặp góc so le giống nhau.
- Tổng số đo của 1 cặp góc trong cùng phía là 180°.
- Số đo 1 cặp góc đồng vị giống nhau.
Tiên đề Euclid về hai đường thẳng song song
Tiên đề Euclid: “Qua một điểm nằm ngoài một đường thẳng, chỉ có duy nhất một đường thẳng song song với đường thẳng đó”.

Tiên đề này giúp chúng ta xác định tính duy nhất của đường thẳng song song qua một điểm cho trước. Đây là tiên đề thứ năm của Euclid và là nền tảng quan trọng để xây dựng nhiều định lý, tính chất trong hình học. Bạn có thể dùng kiến thức này để vẽ hai đường thẳng song song hoặc chứng minh các bài toán hình học.
Tính chất của hai đường thẳng song song
Trong hình học phẳng, nếu hai đường thẳng cùng song song với nhau thì có mối quan hệ đặc biệt khi bị cắt bởi một đường thẳng khác. Nhờ đó, ta có thể suy ra nhiều tính chất quan trọng về tính song song của hai đường thẳng.

Dưới đây là các tính chất hai đường thẳng song song cơ bản:
Trường hợp 1: đường thẳng đi qua 2 đường thẳng song song:
- Số đo của 1 cặp góc so le trong giống nhau.
- Tổng của 2 góc trong nằm cùng một phía là 180° (bù nhau).
- Một cặp góc đồng vị bằng nhau.
Trường hợp 2: Xét 2 đường thẳng bất kỳ, nếu chúng cùng đồng thời song song/vuông góc với 1 đường thẳng khác thì vị trí tương đối của chúng là song song.
Cách vẽ hai đường thẳng song song
Nếu bạn đã hiểu rõ tính chất và dấu hiệu nhận biết hai đường thẳng song song, việc áp dụng vào bài toán sẽ trở nên dễ dàng hơn. Tuy nhiên, để giải bài tập và ứng dụng trong thực tế, bạn cũng cần biết cách vẽ chính xác.
Để vẽ hai đường thẳng song song từ một điểm A và một đường thẳng a cho trước, bạn làm như sau:
- Bước 1: Bạn đặt 1 cạnh góc vuông của ê-ke trùng với a sao cho điểm A nằm trên cạnh huyền.

- Bước 2: Bạn vẽ đường thẳng c theo cạnh huyền của ê-ke.
- Bước 3: Bạn tịnh tiến ê-ke dọc theo c, sao cho cạnh góc vuông ngắn đi qua A.
- Bước 4: Tiếp theo, bạn vẽ đường thẳng b theo cạnh góc vuông đó. Kết quả, ta được 2 đường thẳng a//b.
Cách chứng minh hai đường thẳng song song (Có ví dụ minh họa)
Bạn có thể dùng tính chất và dấu hiệu nhận biết hai đường thẳng song song để chứng minh hai đường thẳng có mối quan hệ song song với nhau. Cụ thể là:

- Chứng minh tổng số đo 2 góc trong cùng phía là 180°.
- Chứng minh số đo 1 cặp góc so le trong giống nhau.
- Chứng minh 1 cặp góc đồng vị bằng nhau.
- Sử dụng tiên đề Euclid.
- Chứng minh 2 đường thẳng khác nhau cùng vuông góc/song song với đường thẳng khác.
Ví dụ: Cho hình vẽ dưới đây, bạn hãy làm theo yêu cầu sau:

- a) Chứng minh tia Ax và Bz song song.
- b) Tìm α để Bz // Cy.
Lời giải:
- a) Ta có: ∠xAB và ∠ABz là 2 góc trong cùng phía với nhau (1)
∠xAB + ∠ABz = 130° + 50° = 180° (2)
Từ 1 và 2 => Ax//Bz
- b) Vì ∠zBC và ∠yCB là 2 góc trong cùng phía của Bz và Cy nên để Bz//Cy thì:
∠zBC + ∠yCB = 180°
=> α + 145° = 180°
=> α = 180° - 145° = 35°.
Vậy để Bz//Cy thì α = 35°.
Bài tập vận dụng
Với việc nắm vững tính chất, dấu hiệu nhận biết và cách chứng minh hai đường thẳng song song, bạn có thể thực hiện các bài toán hình học từ cơ bản đến phức tạp nhất. Hãy tham khảo và rèn luyện một số bài tập về chủ đề này cùng Sforum nhé!
Bài tập 1: Cho ∆ABC có M là trung điểm BC. Vẽ điểm D trên đường thẳng đi qua đoạn AM sao cho MA = MD. Hãy chứng minh: AB // CD.
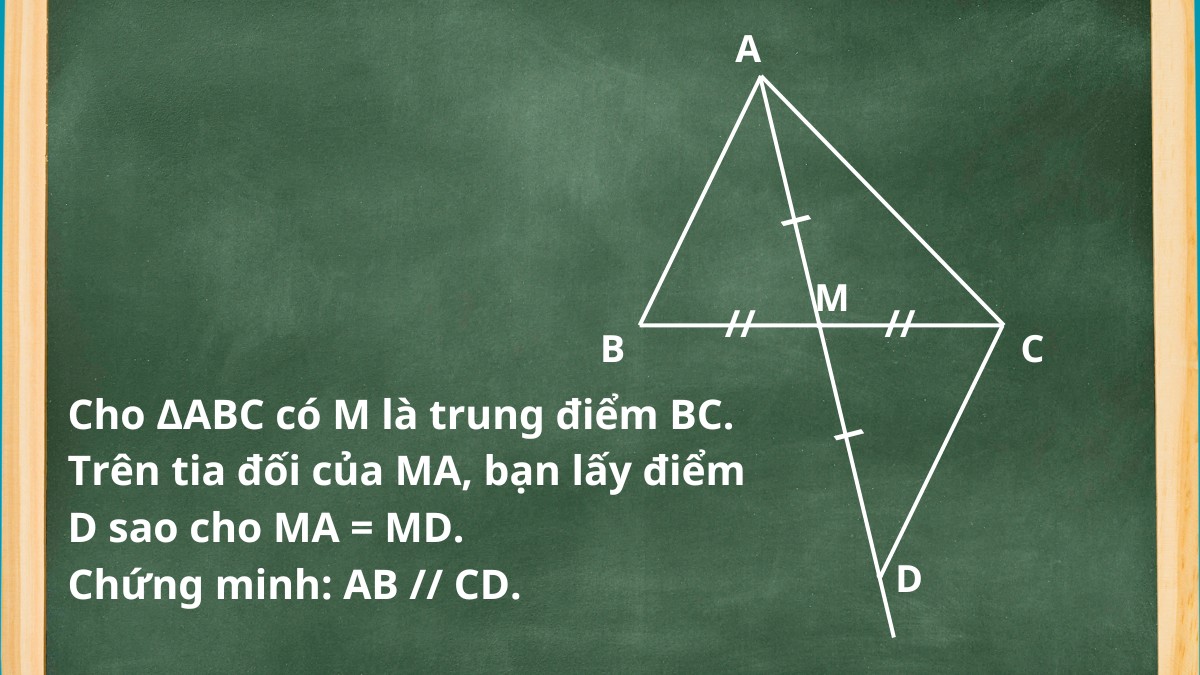
Lời giải:
Xét ∆ABM và ∆DCM ta có:
AM = MD (1)
∠AMB = ∠ DMC (Hai góc đối đỉnh) (2)
BM = MC (M là trung điểm) (3)
Từ 1, 2, 3 => ∆ABM = ∆DCM (c-g-c)
=> ∠ABM = ∠DCM
∠ABM và ∠DCM là 2 góc so le trong của AB, CD => AB // CD.
Bài tập 2: Cho ∆ABC cân tại A, vẽ 2 điểm D và E trên 2 cạnh AB, AC sao cho AD = AE. Bạn hãy chứng minh DE // BC.

Lời giải:
Theo giả thuyết, AD = AE => ∆ADE cân tại A
=> ∠ADE = (180° - ∠DAE)/2 (1)
∆ABC cân tại A => ∠ABC = (180° - ∠BAC)/2 (2)
Từ 1 và 2 => ∠ADE = ∠ABC
Mà ∠ADE và ∠ABC là hai góc đồng vị => DE // BC.
Sforum vừa giới thiệu đến bạn thông tin về tính chất, dấu hiệu nhận biết và cách chứng minh hai đường thẳng song song. Đây là nền tảng hữu ích giúp bạn dễ dàng tiếp cận các bài toán hình học. Hy vọng bài viết sẽ giúp bạn hiểu rõ và áp dụng tốt vào thực tế cũng như học tập nhé!








Bình luận (0)