Hình lập phương là gì? Tính chất và các công thức liên quan


Không ít người thắc mắc hình lập phương là gì mà được sử dụng phổ biến trong toán học và đời sống. Nội dung bài viết sẽ hướng dẫn bạn cách tính diện tích xung quanh, thể tích và diện tích toàn phần. Thông qua đó, bạn không chỉ giải quyết được các bài toán hình học phức tạp mà còn vận dụng được trong cuộc sống.
Hình lập phương là gì?
Đây là một thuật ngữ chỉ một hình khối ba chiều đặc biệt có tất cả sáu mặt là các hình vuông có kích thước bằng nhau. Mỗi cạnh của hình lập phương đều có chiều dài bằng nhau, và tất cả các góc giữa các mặt đều là góc vuông.
Đây được coi là một khái niệm rất quan trọng trong hình học không gian cũng các lĩnh vực khác trong đời sống hàng ngày. Những công thức như tính thể tích, diện tích xung quanh và diện tích toàn phần hình lập phương giúp giải quyết nhiều vấn đề thực tế và hỗ trợ học sinh trong quá trình học tập hiệu quả.

Tính chất hình lập phương là gì?
Hình lập phương là một dạng khối quen thuộc, thường gặp trong toán học và đời sống thực tế. Các công thức liên quan đến thể tích, diện tích xung quanh, và diện tích toàn phần hình lập phương không chỉ hỗ trợ việc giải bài tập hình học mà còn được áp dụng trong nhiều tình huống thực tiễn đáng chú ý.
- Các mặt của hình lập phương đều là hình vuông: có sáu mặt, tất cả đều là những hình vuông có diện tích bằng nhau. Đặc trưng này là điểm hình thành nên sự đối xứng trong khối lập phương.
- Các cạnh có chiều dài bằng nhau: Tất cả 12 cạnh của hình đều có cùng chiều dài, mang lại sự đồng nhất cho toàn bộ khối hình.
- Các góc vuông: Mỗi góc giữa hai cạnh là 90 độ, điều này tạo thành góc vuông tại mỗi điểm giao nhau của các cạnh.
- Tính đối xứng cao: Khối lập phương có thể xoay quanh các trục của nó mà không thay đổi hình dạng.
- Các đường chéo đều bằng nhau: Mỗi đường chéo của hình lập phương kết nối các đỉnh đối diện và có độ dài giống nhau.

Những công thức tính khối lập phương
Khối lập phương là một dạng khối quen thuộc, dễ nhận biết với tính đối xứng hoàn hảo. Các công thức tính diện tích xung quanh, thể tích và diện tích toàn phần không chỉ giúp giải quyết các bài toán mà còn có nhiều ứng dụng thiết thực trong cuộc sống hàng ngày. Với tính chất đồng nhất của các cạnh, giả sử chiều dài cạnh là a, ta có thể dễ dàng suy ra các công thức quan trọng:
Công thức tính chu vi
Chu vi hình lập phương được tính bằng cách cộng tổng chiều dài của 12 cạnh, đây là công thức cơ bản nhưng hữu ích khi làm bài tập hoặc vận dụng vào những tình huống thực tế.
P = 12 × a
Ví dụ: Nếu hình lập phương có cạnh dài 4cm, chu vi của nó sẽ là:
P = 12 × 4 = 48cm

Công thức tính diện tích
Diện tích xung quanh hình lập phương được hiểu là tổng diện tích của bốn mặt bên, không bao gồm diện tích mặt đáy và mặt trên. Công thức này đặc biệt hữu ích khi bạn chỉ cần quan tâm đến phần bao quanh của hình mà không tính toàn bộ bề mặt.

Trong khi đó, diện tích toàn phần hình lập phương là diện tích của tất cả sáu mặt. Công thức tính diện tích toàn phần là:

Ví dụ: Với hình ABCD có cạnh dài 5cm, diện tích xung quanh là:
Sxq = 4 × 5² = 100cm²
Và diện tích toàn phần là: Stp = 6 × 5² = 150cm²
Công thức tính thể tích
Thể tích hình lập phương biểu thị lượng không gian mà nó chiếm trong không gian ba chiều. Để tính toán giá trị này, bạn chỉ cần biết chiều dài của một cạnh duy nhất. Nhờ vậy, việc giải bài toán này trở nên đơn giản và nhanh chóng, ngay cả khi bạn mới bắt đầu làm quen với hình học không gian.

Ví dụ: Nếu một khối lập phương có cạnh dài 6cm, thể tích của nó sẽ là:
V = 6³ = 216cm³
Nếu bạn đang tìm kiếm công cụ hỗ trợ học tập về hình lập phương, một chiếc laptop cấu hình cao tại CellphoneS sẽ là lựa chọn lý tưởng nhất. Nhờ đó, bạn nghiên cứu thêm về các công thức liên quan như diện tích xung quanh, thể tích và diện tích toàn phần. Đồng thời, bạn có thể tính toán chính xác và tìm hiểu các khái niệm hình học một cách dễ dàng hơn.
[Product_Listing categoryid="380" propertyid="" customlink="https://cellphones.com.vn/laptop.html" title="Danh sách Laptop đang được quan tâm nhiều tại CellphoneS"]
Hướng dẫn vẽ hình lập phương đơn giản
Hình lập phương là dạng hình khối quen thuộc trong toán học và thực tế đời sống. Chỉ với vài thao tác cơ bản, bạn có thể hoàn thành việc vẽ khối lập phương trong thời gian ngắn.
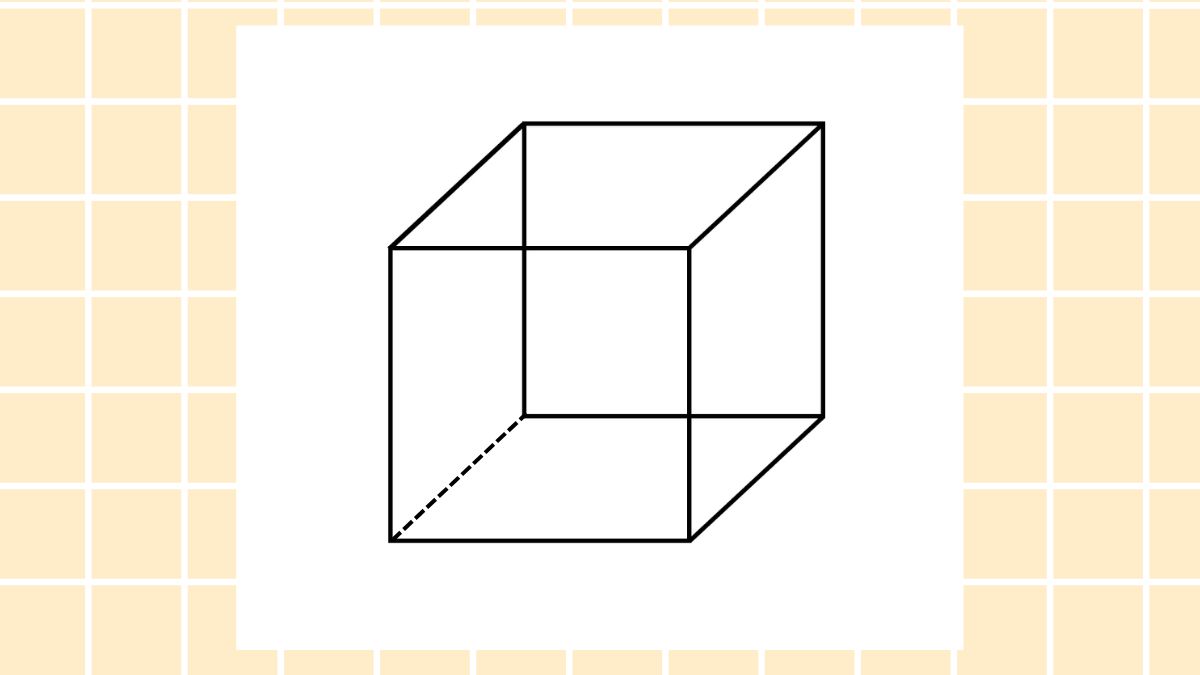
Bước 1: Vẽ một hình vuông, hình này sẽ đóng vai trò là mặt trước.

Bước 2: Vẽ thêm một hình vuông thứ hai phía sau và hơi lệch về bên trên.

Bước 3: Nối các đỉnh tương ứng của hai hình vuông bằng đoạn thẳng để tạo thành khối lập phương hoàn chỉnh. Đối với đường nào không nhìn thấy thì trình bày bằng nét đứt.
Một số bài tập thường gặp
Để hiểu rõ hơn về các công thức và đặc điểm của khối lập phương, việc luyện tập qua các bài tập thực tế sẽ giúp bạn áp dụng kiến thức một cách hiệu quả. Sau đây là ba bài tập giúp bạn củng cố và nâng cao khả năng tính toán về diện tích xung quanh, thể tích và diện tích toàn phần hình lập phương.
Bài tập 1: Một hình lập phương có cạnh dài 8 cm. Hãy tính thể tích, diện tích xung quanh, và diện tích toàn phần hình này.

Bài tập 2: Tìm chiều dài cạnh của một hình lập phương nếu thể tích của nó là 729 cm³.

Bài tập 3: Một khối lập phương có diện tích toàn phần là 486 cm². Tính thể tích của hình này.

Ứng dụng của hình lập phương trong cuộc sống
Trong thực tiễn, khối lập phương trong hình học không gian là một chuyên đề cơ bản nhưng cũng không kém phần thiết yếu trong nhiều lĩnh vực khác nhau. Những ứng dụng này có mặt trong mọi lĩnh vực từ công nghiệp, thiết kế cho đến đời sống hàng ngày. Các ứng dụng phổ biến bao gồm:
- Trong xây dựng: Hình lập phương thường được dùng trong các thiết kế kiến trúc, đặc biệt là trong việc tính toán diện tích và thể tích các khối nhà hay các công trình hình khối.
- Trong thiết kế sản phẩm: Những vật dụng như hộp lưu trữ, thùng đựng hàng, hay bao bì thường có hình dáng hình lập phương để tận dụng tối đa không gian lưu trữ và đảm bảo sự tiện lợi trong vận chuyển.
- Trong các trò chơi: Các viên xúc xắc, là một ví dụ điển hình của khối lập phương, được sử dụng phổ biến trong các trò chơi giải trí.
- Trong nghệ thuật và sáng tạo thiết kế: Các tác phẩm nghệ thuật ba chiều thường sử dụng hình lập phương như một yếu tố tạo điểm nhấn, giúp nâng cao giá trị thẩm mỹ và tạo cảm giác không gian độc đáo.
- Trong công nghiệp: Sử dụng khối lập phương giúp tối ưu hóa không gian, chẳng hạn như trong việc tính toán không gian lưu trữ và vận chuyển hàng hóa.

Qua bài viết, bạn đã hiểu rõ hình lập phương là gì trong toán học. Với những kiến thức cơ bản như công thức tính diện tích xung quanh, thể tích, diện tích toàn phần hình lập phương, bạn sẽ dễ dàng vượt qua các bài toán hình học cũng như vận dụng vào thực tế. Hy vọng bài viết này sẽ là nguồn tài liệu hữu ích trong quá trình học tập và tìm hiểu!








Bình luận (0)