Hình ngũ giác - Các công thức và bài tập vận dụng

Hình ngũ giác không chỉ liên quan đến lĩnh vực toán học mà còn được sử dụng rộng rãi trong thực tiễn. Việc tính diện tích hình ngũ giác đóng vai trò quan trọng khi cần đo đạc hoặc thiết kế. Nếu bạn muốn nắm rõ công thức tính diện tích chính xác, Sforum sẽ hướng dẫn chi tiết ngay sau đây.

Định nghĩa của hình ngũ giác

Trước khi đào sâu vào phần công thức tính diện tích hình ngũ giác và các bài toán thì chúng ta sẽ cùng tìm hiểu qua định nghĩa của nó. Hình ngũ giác là một đa giác có năm cạnh và năm góc. Tùy vào độ dài các cạnh và góc mà hình này được chia thành hai loại: ngũ giác đều (có các cạnh và góc bằng nhau) và ngũ giác không đều.

Hình ngũ giác đều có tính đối xứng cao và thường xuất hiện trong thiết kế, kiến trúc, mô hình toán học. Ngược lại, hình ngũ giác không đều có thể có kích thước cạnh khác nhau, khiến việc tính diện tích và chu vi phức tạp hơn.

Để dễ dàng hơn trong việc cập nhật cái kiến thức toán học mới như hình ngũ giác,... thì bạn nên trang bị một chiếc iPad để thuận tiện hơn cho việc học hành. Hãy xem ngay những dòng iPad đang được yêu thích tại CellphoneS dưới đây: 

[Product_Listing categoryid="944" propertyid="" customlink="https://cellphones.com.vn/tablet/ipad.html" title="Các mẫu iPad đang được quan tâm nhiều tại CellphoneS"]

Các công thức tính toán của hình ngũ giác

Hình ngũ giác có nhiều cách để tính diện tích và chu vi. Nếu biết độ dài cạnh hoặc các yếu tố liên quan, bạn có thể dễ dàng xác định các thông số cần thiết. Bạn hãy cùng Sforum xem qua các công thức tính hình ngũ giác sau nhé.

Cách tính chu vi của hình ngũ giác

Để tính chu vi, ta cần lấy tổng độ dài của tất cả các cạnh của hình. Đối với hình ngũ giác không đều, công thức sẽ là tính như sau:

P=a+b+c+d+e

Nếu là hình ngũ giác đều, việc xác định chu vi sẽ trở nên dễ dàng hơn.

P= 5 . a

Trong đó:

• P là chu vi
• a, b, c, d, e là cạnh của hình ngũ giác

Cách tính diện tích hình ngũ giác

Việc tính diện tích hình ngũ giác phụ thuộc vào loại ngũ giác bạn đang xét. Với hình ngũ giác đều, công thức tính diện tích là: 

Trong đó:

• S là diện tích hình ngũ giác đều
• a là độ dài cạnh

Có nhiều cách để tính diện tích hình ngũ giác không đều, trong đó một phương pháp phổ biến là chia hình thành các tam giác nhỏ hơn, sau đó tính tổng diện tích của chúng.

• Phương pháp tính diện tích ngũ giác: 

Chọn một đỉnh bất kỳ và vẽ các đường chéo nối với các đỉnh khác, ta sẽ phân chia ngũ giác thành các tam giác nhỏ. Khi đó, tổng diện tích của ngũ giác sẽ bằng tổng diện tích của các tam giác này, giúp việc tính toán trở nên dễ dàng hơn. Công thức tính diện tích tam giác:

S=12.d.h

Trong đó: 

• • d: chiều dài cạnh
  • h: chiều cao

• Phương pháp Heron để tính diện tích hình ngũ giác: 

Trong đó: 

• S là diện tích hình ngũ giác
• a, b, c, d, e là các cạnh của ngũ giác 
• s là nửa chu vi của hình ngũ giác

Hướng dẫn vẽ hình ngũ giác đều

Vẽ một hình ngũ giác đều không quá khó nếu bạn áp dụng đúng cách.Bạn có thể áp dụng compa, thước đo góc hoặc công cụ vẽ hình học để kiểm tra và đảm bảo độ chính xác của các cạnh và góc. Sforum sẽ hướng dẫn bạn vẽ ngũ giác đều bằng compas như sau: 

Bước 1: Vẽ một đường tròn có tâm O. Vẽ 2 đường kính AB và CD, xác định M là trung điểm của bán kính 

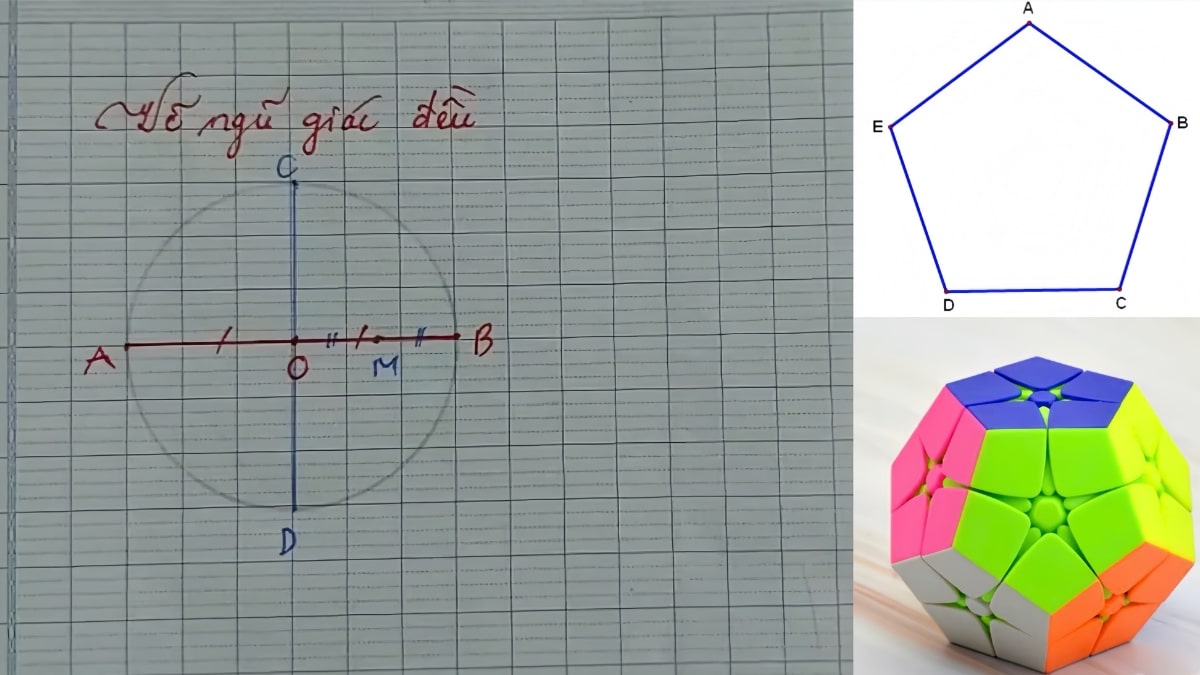
Bước 2: Tiếp đến, vẽ cung tròn tâm M, bán kính MC. Cung tròn cắt OA tại điểm N. 

Bước 3: Điều chỉnh compba bằng với đoạn CN, rồi đánh dấu trên các điểm của cung đường tròn

Bước 4: Nối các điểm theo thứ tự để hoàn thiện hình ngũ giác đều với năm cạnh bằng nhau và góc đều nhau.

Việc vẽ đúng hình ngũ giác đều giúp bạn dễ dàng tính diện tích, chu vi và ứng dụng trong thiết kế hoặc trang trí.

Một số bài tập vận dụng về hình ngũ giác

Các bài toán thực tế sẽ giúp bạn dễ dàng nắm bắt cách tính diện tích hình ngũ giác cũng như chu vi của cả hình ngũ giác đều và không đều. Thông qua những bài tập này, bạn có thể áp dụng công thức một cách linh hoạt và chính xác.

Bài tập 1: Tính diện tích hình ngũ giác 

Cho hình ngũ giác đều có cạnh a = 8cm. Tính diện tích hình ngũ giác đều này

Lời giải: 

Bài tập 2: Tính diện tích ngũ giác không đều 

Cho hình ngũ giác có cạnh lần lượt là 2 cm, 4 cm, 5 cm, 3 cm, 5 cm. Tính diện tích hình ngũ giác này

Lời giải: 

Nửa chu vi hình ngũ giác là:

Áp dụng phương pháp Heron, ta có: 

Bài tập 3: Tính chu vi hình ngũ giác 

Cho hình ngũ giác có cạnh lần lượt là 2 cm, 4 cm, 5 cm, 3 cm, 5 cm. Hãy tính chu vi hình ngũ giác không đều sau

Lời giải: 

P=2+4+5+3+5=19 cm

Hình ngũ giác được áp dụng rộng rãi trong đời sống, bao gồm cả lĩnh vực thiết kế và toán học. Việc nắm vững cách tính diện tích hình ngũ giác và chu vi giúp bạn dễ dàng giải quyết bài toán và áp dụng vào thực tế..Đặc biệt, đối với hình ngũ giác đều, việc tính toán sẽ dễ dàng hơn, giúp rút ngắn thời gian thực hiện. Mong rằng hướng dẫn từ Sforum sẽ đem lại cho bạn những kiến thức giá trị về loại hình học này cũng như các bài viết giáo dục.

Đọc bài viết cùng chuyên mục: Góc Học & Dạy 4.0