Hình thang là gì? Công thức tính diện tích hình thang

Hình thang luôn là một chủ đề nhiều người muốn tìm hiểu trong toán học. Để hiểu rõ hơn về các đặc điểm của nó, việc nắm vững cách tính chu vi, diện tích hình thang cân, vuông… là rất cần thiết. Ở bài viết dưới đây, Sforum sẽ chỉ bạn các công thức cơ bản để bạn có thể áp dụng vào quá trình học của mình.

Hình thang là gì?

Hình thang là loại tứ giác với 2 cạnh trên dưới song song, trong khi 2 cạnh kia không như vậy. Dựa vào đặc điểm cạnh trên, cộng thêm góc, nó có thể được phân thành các loại khác nhau như thang cân, vuông… Trong toán học, loại tứ giác này có nhiều ứng dụng và thường xuất hiện trong những bài toán về diện tích, chu vi.

Sau khi hiểu rõ về các đặc điểm và cách tính chu vi, diện tích hình thang cân, việc áp dụng vào bài tập sẽ trở nên dễ dàng hơn. Để học tập hiệu quả hơn, bạn có thể tham khảo các mẫu iPad tại CellphoneS – thiết bị hỗ trợ đắc lực giúp bạn tra cứu kiến thức và thực hành mọi lúc mọi nơi.

[Product_Listing categoryid="944" propertyid="" customlink="https://cellphones.com.vn/tablet/ipad.html" title="Các mẫu iPad đang được quan tâm nhiều tại CellphoneS"]

Dấu hiệu nhận biết hình thang

Khi nắm vững các dấu hiệu nhận biết hình thang sẽ là "chìa khóa vàng" để bạn tự tin đối mặt với các bài toán hình học khó.

• Cạnh đáy song song: Đặc trưng của hình thang là cặp cạnh song song.
• Góc kề một cạnh đáy: Nếu hai góc kề cùng một cạnh bên có tổng bằng 1800, tứ giác đó là hình thang.
• Đối xứng: Với hình thang cân sẽ có cạnh bên, góc kề cạnh đáy độ dài bằng nhau.

Tính chất về hình thang

Tính chất góc và cạnh của hình thang là những yếu tố quan trọng để nhận biết và phân loại loại tứ giác đặc biệt này. Một trong những tính chất nổi bật là hai cạnh đáy song song, khiến cho tổng hai góc kề một cạnh bên luôn bằng.

Trong hình thang cân, góc kề mỗi cạnh đáy có số đo như nhau và hai cạnh ở phía hai bên cũng như vậy là tính chất dễ nhận diện của tứ giác đặc biệt này. Nhờ đó mà hình thang giữ vai trò quan trọng, thiết yếu khi vận dụng vào các bài toán cũng như trong thực tế.

Các dạng đặc biệt về hình thang

Các loại hình thang đặc biệt có những dấu hiệu nhận biết riêng, giúp chúng ta phân loại và áp dụng hơn trong bài toán hình học. 

• Hình thang vuông: Có một góc 90º
• Hình thang cân: Có tính đối xứng khi cạnh bên và góc kề đáy bằng nhau.
• Hình bình hành: Cạnh đối có đặc điểm bằng chiều dài nhau, song song.
• Hình chữ nhật: Một dạng hình thang kết hợp giữa tính chất cân đối và các góc vuông, tạo nên hình thang vừa cân vừa có các góc vuông.

Công thức tính chu vi hình thang

Để xác định được cách tính chu vi hình thang, bạn nên “note” lại các công thức sau: 

Chu vi hình thang thường:

• Công thức: P = a + b + c + d

• Chú thích: a, b: 2 cạnh đáy, c, d: 2 cạnh bên

Chu vi hình thang vuông:

• Công thức: P = a + b + c + d

• Chú thích: a, b: 2 cạnh đáy, c: cạnh bên vuông góc với đáy, d: đường còn lại

Chu vi hình thang cân: 

• Công thức: P =  (2 x a) + b + c

• Chú thích: a, b: cạnh đáy, c: cạnh bên

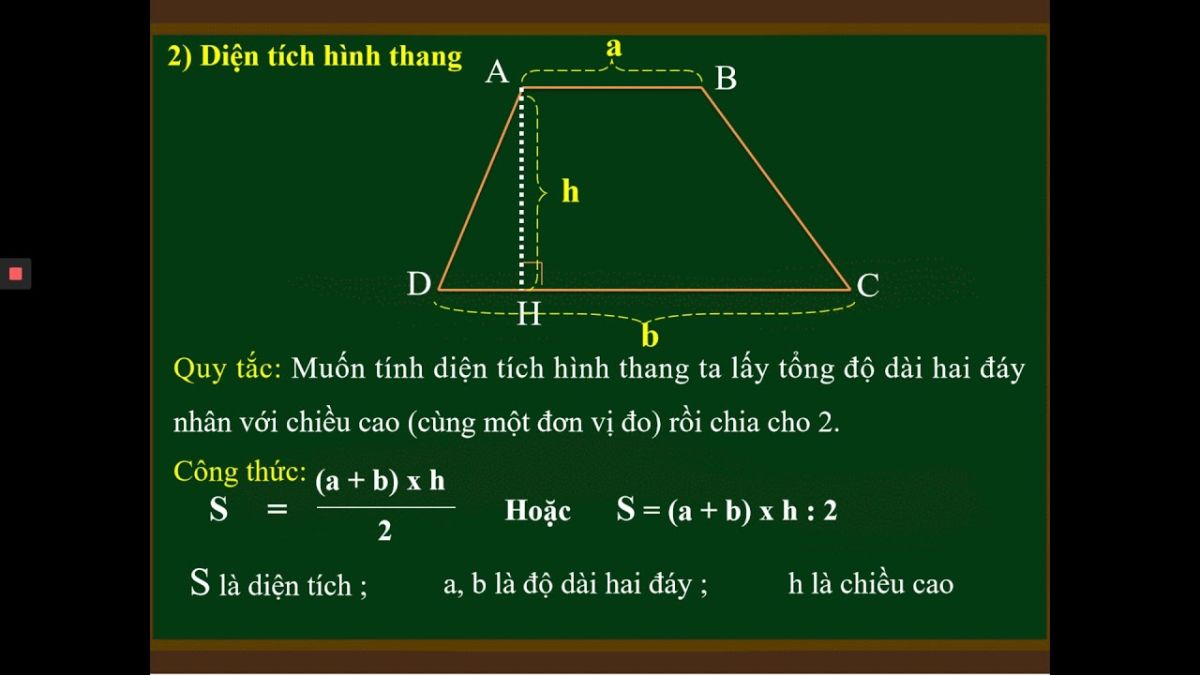
Công thức tính diện tích hình thang

Tùy thuộc vào hình dạng đặc biệt của từng loại, việc tính diện tích hình thang sẽ có những phương pháp khác nhau.

Cách tính S hình thang thường:

• Công thức: S = ((a + b) *h)/2 
• Chú thích: a, b: cạnh đáy, h: chiều cao

Cách tính S hình thang cân:

• Công thức: S =  ((a + b) *h)/2 

• Chú thích: Hình thang cân có hai cạnh bên bằng nhau và các góc kề hai cạnh đáy bằng nhau, nhưng diện tích vẫn tính theo công thức chung, với h là khoảng cách vuông góc giữa hai đáy.

Cách tính S hình thang vuông:

• Công thức: S = ((a + b) *h)/2 

• Chú thích: Hình thang vuông có một góc vuông, vì vậy chiều cao h chính là cạnh bên vuông góc với hai đáy a và b.

Một số dạng bài tập về hình thang

Để áp dụng các kiến thức về hình thang vào thực tế, việc luyện tập qua các bài tập là vô cùng quan trọng. Hãy để bản thân chinh phục và thử sức với những bài tập về tính chu vi, diện tích hình thang cân, vuông... cực kỳ thú vị này nhé!

Dạng bài tính số đo góc

Đối với bài toán tính góc trong hình thang, chúng ta thường sử dụng tính chất về góc kề của hình thang.

Đề bài: Cho hình thang ABCD có đáy AB//CD và góc D = 70º. Tính góc C .

Lời giải: Như chúng ta đã biết thông tin ở trên thì hai góc kề có tổng là 180º. Từ đó, chúng ta suy ra: Góc C = 180º - 70º = 110º

Dạng bài chứng minh hình thang/ hình thang cân/ hình thang vuông

Bài toán dạng này thường yêu cầu chứng minh một tứ giác là hình thang hoặc phân loại các loại hình thang dựa vào tính chất cạnh và góc.

Đề bài: Cho hình tứ giác ABCD có đặc điểm AB//CD cộng với AD = BC. Chứng minh rằng hình tứ giác này là hình thang cân.

Lời giải: Do đạc điểm AB//CD nên ABCD chắc chắn là hình thang. Ngoài ra, do AD = BC nên chắc chắn có 2 cạnh bằng nhau, vì vậy ABCD là hình thang cân.

Dạng bài áp dụng tính chất và chứng minh yêu cầu của đề

Dạng bài này thường yêu cầu sử dụng tính chất đặc trưng của hình thang để chứng minh các mệnh đề trong đề bài.

Đề bài: Cho ABCD là hình thang có đặc điểm AB//CD cộng với cạnh AD = BC. Hãy làm rõ và chứng minh △ABD đồng dạng với △CDB

Lời giải: Trong hình thang ABCD có AB//CD nên 2 góc ADB = CBD. Hơn nữa, AD = BC, chứng tỏ △ABD đồng dạng với △CDB theo trường hợp góc - cạnh - góc.

Dạng bài tính diện tích, chu vi

Với dạng bài tập này, bạn sẽ được làm quen với nhiều cách tính chu vi, diện tích của các loại hình thang khác nhau.

Đề bài: Cho hình thang ABCD với AB =8cm, CD = 12cm, cạnh bên AD = 6cm, BC = 7cm, h = 5cm. Xác định S và P.

Lời giải: 

• Diện tích: S =((8 + 12) *5)/2 = (20 *5)/2 = 50 cm²
• Chu vi: P = 8 + 12 + 6 + 7 = 33 cm.

Qua những thông tin trên, hy vọng bạn đã nắm vững những kiến thức cơ bản về hình thang, từ đặc điểm đến các công thức quan trọng. Việc hiểu rõ cách tính chu vi, diện tích hình thang cân sẽ giúp bạn dễ dàng đối mặt khi gặp các bài toán khó. Hãy biến việc học toán thành một cuộc phiêu lưu thú vị khi ghi nhớ các thông tin trên nhé! Tham khảo thêm danh mục "mẹo vặt" của Sforum để cập nhật thêm nhiều kiến thức mới khác nhé.