Hình lăng trụ đều là gì? Có bao nhiêu loại lăng trụ đều?

Lăng trụ đều là một trong những hình học không gian đặc biệt, với đặc điểm nổi bật là hai đáy có hình dạng đa giác đều, vừa bằng nhau lại song song với nhau. Các mặt bên của hình lăng trụ đều là những hình chữ nhật đều, được sắp xếp một cách hoàn hảo để tạo ra sự đối xứng tuyệt đối. Qua bài viết này, hãy cùng Sforum tìm hiểu chi tiết về đặc điểm, công thức và ứng dụng của hình lăng trụ đều.

Định nghĩa của hình lăng trụ đều

Lăng trụ đều là một khái niệm đầy thú vị trong hình học không gian 3D, nơi mà sự kết hợp hoàn hảo giữa các yếu tố hình học tạo ra một cấu trúc vững chắc và đối xứng. Hình lăng trụ được hình thành từ một hình đa giác đều làm nền, với những cạnh thẳng nối từ các đỉnh của đa giác đó lên một điểm chung. Điểm này nằm trên một đường thẳng song song với mặt phẳng của đa giác nền, tạo nên một kết cấu độc đáo, hài hòa và cân đối.

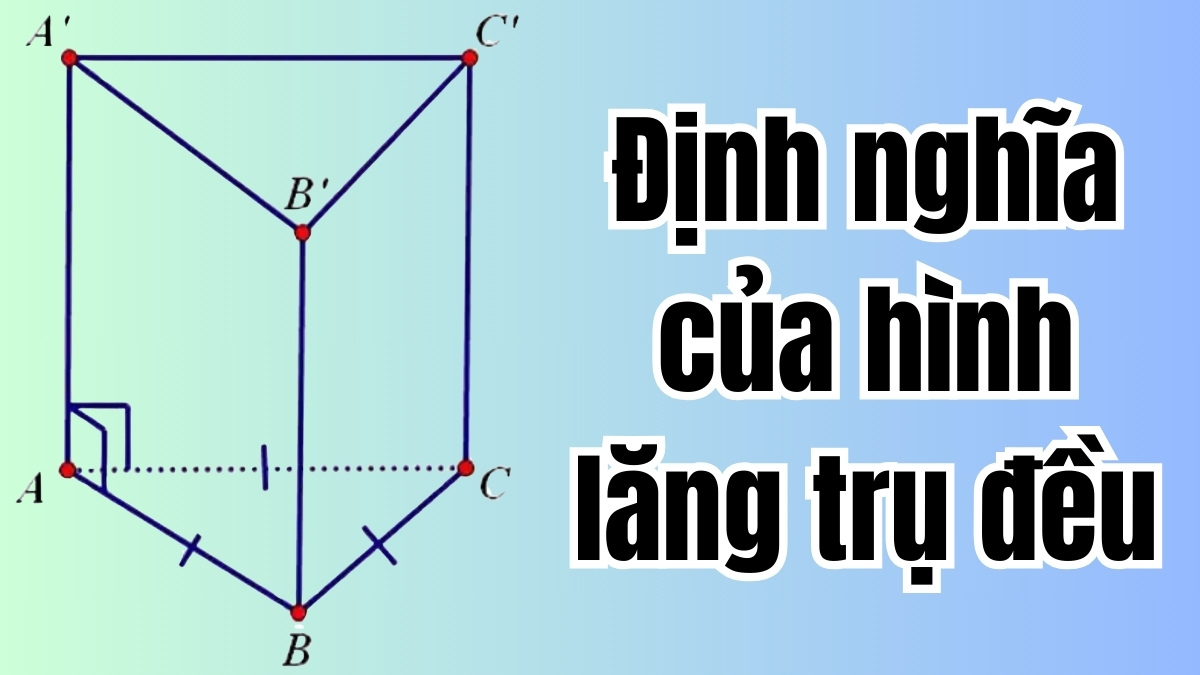
Mỗi đỉnh của hình lăng trụ đều có độ cao bằng nhau so với mặt nền, đồng thời tất cả các đỉnh đều nằm trên một mặt phẳng song song với mặt đa giác, mang đến sự đối xứng hoàn hảo và cân đối.

Nếu bạn đang tìm kiếm một chiếc laptop để học và tìm hiểu về khối lăng trụ đều là gì, hãy chọn một chiếc máy tính có hiệu suất ổn định và màn hình sắc nét. Một laptop với cấu hình vừa đủ, RAM 8GB và màn hình từ 14 inch trở lên sẽ giúp bạn dễ dàng truy cập tài liệu học tập. Việc sở hữu một chiếc laptop tốt không chỉ giúp bạn học hiệu quả mà còn tạo điều kiện thuận lợi để khám phá các ứng dụng hình học trong thực tế.

[Product_Listing categoryid="380" propertyid="" customlink="https://cellphones.com.vn/laptop.html" title="Danh sách Laptop đang được quan tâm nhiều tại CellphoneS"]

Lăng trụ đều có đặc điểm gì?

Hình lăng trụ đều sở hữu những đặc điểm vô cùng ấn tượng, thể hiện sự hoàn hảo và tính đối xứng trong không gian ba chiều. Điểm đặc biệt nổi bật của lăng trụ đều chính là cấu trúc đối xứng và cân đối của nó. 

Hai mặt đáy của lăng trụ là những đa giác đều, không chỉ đồng dạng mà còn có kích thước hoàn toàn bằng nhau, tạo nên sự cân đối hoàn hảo trong không gian ba chiều. Các cạnh bên của lăng trụ đều là những đoạn thẳng song song, với độ dài hoàn toàn đồng nhất, tạo nên một cấu trúc vững chắc và đối xứng tuyệt đối.

Mỗi cạnh của đa giác đáy trong lăng trụ đều được nối với một điểm tương ứng nằm trên một đường thẳng song song với mặt đáy, tạo nên sự liên kết chặt chẽ và đảm bảo tính đối xứng hoàn hảo trong không gian ba chiều. 

Đặc biệt, độ cao của các đỉnh thuộc đa giác đáy luôn bằng nhau, góp phần tạo nên một tổng thể hài hòa và cân đối. Cuối cùng, góc giữa các cạnh bên và mặt đáy luôn là góc vuông, mang lại sự vững chãi và chắc chắn cho hình khối này. 

Các loại hình lăng trụ đều phổ biến và thường gặp

Các khối lăng trụ đều phổ biến và thường gặp chủ yếu phụ thuộc vào hình dạng của đa giác đáy. Mỗi loại hình lăng trụ đều có những đặc điểm riêng biệt nhưng vẫn giữ được tính chất đối xứng và đều đặn của hình lăng trụ. Dưới đây là một số loại lăng trụ đều, mà bạn có thể tham khảo qua:

Lăng trụ tam giác đều

Lăng trụ tam giác đều là một hình học không gian độc đáo, nổi bật với hai đáy là hai hình tam giác đều, không chỉ đồng dạng mà còn hoàn toàn giống nhau về kích thước và hình dáng. Đặc điểm nổi bật của nó là đáy có ba cạnh bằng nhau và ba góc 60 độ. Các cạnh bên của lăng trụ là những đoạn thẳng song song, có độ dài đồng nhất, tạo thành các mặt bên là những hình chữ nhật hoàn hảo. Chiều cao của lăng trụ là khoảng cách vuông góc giữa hai đáy, một yếu tố quan trọng giúp tạo nên sự vững chắc và ổn định cho hình khối.

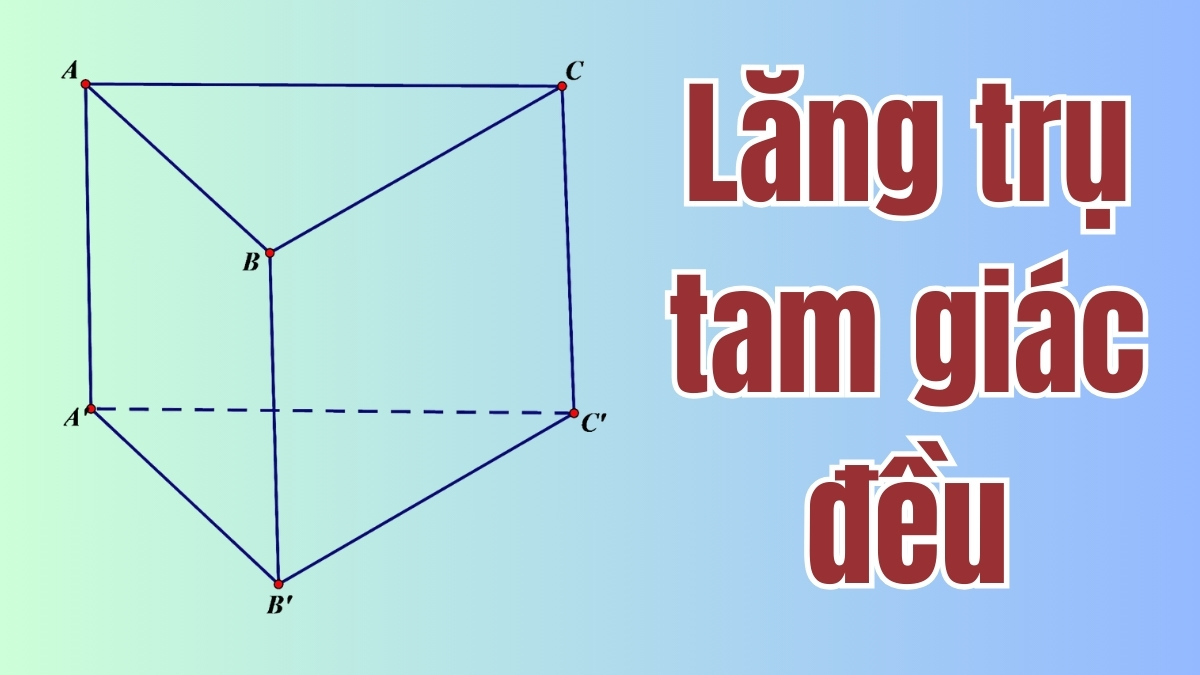
Trong kiến trúc, hình dáng đặc biệt của lăng trụ tam giác đều tạo nên những công trình độc đáo, có sự cân đối và tính thẩm mỹ cao, đồng thời giúp tối ưu hóa không gian - kết cấu. Ngoài ra, nó còn được sử dụng trong mô hình hóa 3D, thiết kế đồ họa - trò chơi, mang lại sự thẩm mỹ và tính vững chắc cho các hình khối.

Lăng trụ tứ giác đều

Lăng trụ tứ giác đều là một hình học không gian đặc biệt, nổi bật với hai đáy là hai hình vuông đều, hoàn toàn đồng nhất về kích thước và hình dáng. Đặc điểm nổi bật của nó là đáy có bốn cạnh bằng nhau và bốn góc vuông 90 độ. Các cạnh bên có chiều dài đồng đều, tạo thành các mặt bên là hình chữ nhật khi nhìn từ bên cạnh. Chiều cao của lăng trụ là khoảng cách vuông góc giữa hai đáy và hình học này có tính đối xứng cao với nhiều trục đối xứng qua các đỉnh của đáy.

Với cấu trúc vững chãi và đối xứng hoàn hảo, lăng trụ tứ giác đều trở thành lựa chọn lý tưởng trong thiết kế các công trình có yêu cầu về sự bền vững. Nó cũng được sử dụng trong cơ học để tối ưu hóa cấu trúc chịu lực và trong mô hình hóa 3D cho thiết kế đồ họa và các trò chơi kỹ thuật số.

Lăng trụ lục giác đều

Đặc điểm của lăng trụ lục là đáy có sáu cạnh bằng nhau và sáu góc 120 độ. Các cạnh bên của lăng trụ có chiều dài đồng đều, tạo thành các mặt bên là hình chữ nhật khi nhìn từ bên cạnh. Chiều cao của lăng trụ là khoảng cách vuông góc giữa hai đáy và hình học này có tính đối xứng cao với nhiều trục đối xứng qua các đỉnh của đáy.

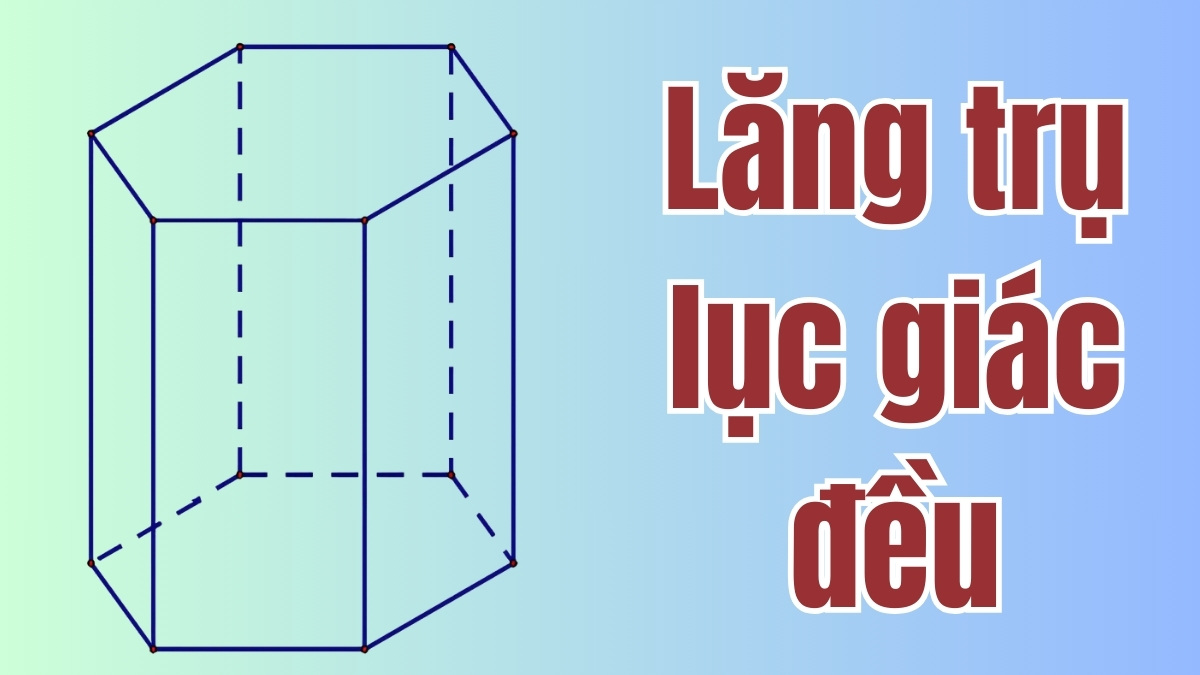
Lăng trụ lục giác đều không chỉ là một hình học không gian thú vị mà còn có những ứng dụng thực tiễn đầy sáng tạo trong kiến trúc. Nó cũng được sử dụng trong cơ học để tối ưu hóa cấu trúc chịu lực - trong mô hình hóa 3D, thiết kế đồ họa, trò chơi, mang lại tính thẩm mỹ và độ vững chắc cho các hình khối.

Các công thức liên quan tới lăng trụ đều

Lăng trụ đều là một hình học đặc trưng với các đặc điểm dễ nhận diện như có đáy là một đa giác đều và các cạnh bên song song, đồng thời có chiều cao đồng đều. Dưới đây là những công thức cơ bản và quan trọng về lăng trụ đều mà bạn cần nắm vững:

Công thức tính diện tích xung quanh lăng trụ đều

Khi nghiên cứu về hình lăng trụ đều, một trong những thông số quan trọng mà chúng ta cần tính toán là diện tích xung quanh. Cụ thể có công thức như sau:

S xq = P đáy x h

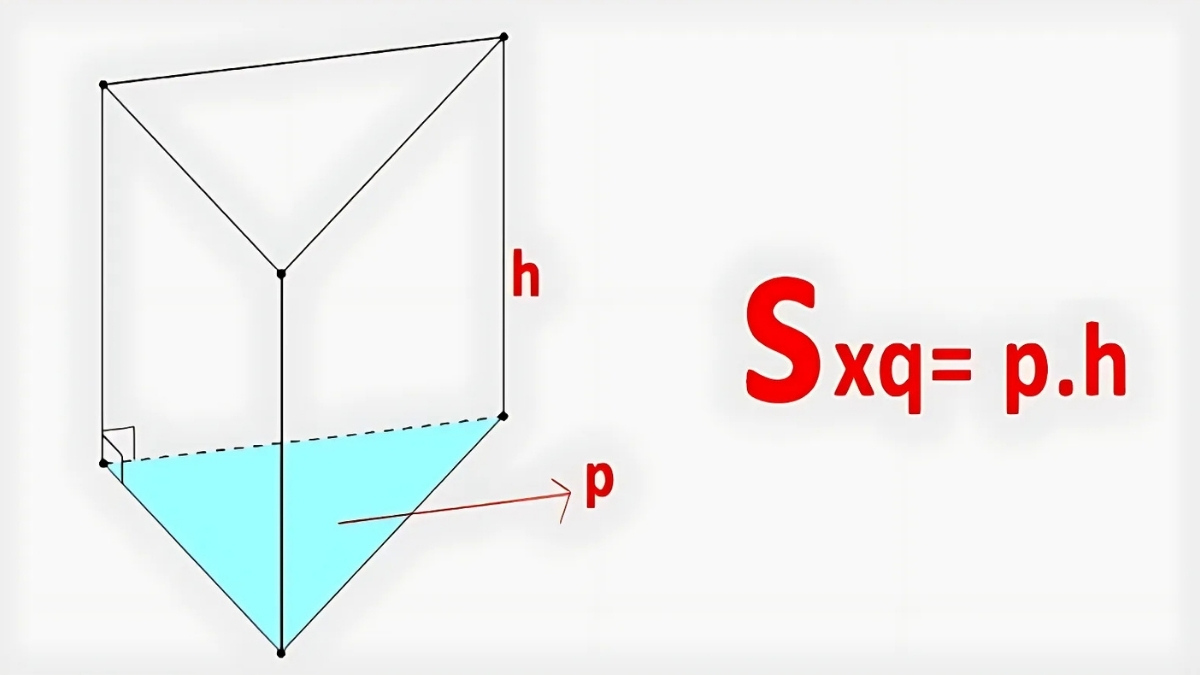
Trong đó: 

P đáy: là chu vi của đáy (tính bằng n × a, với n là số cạnh của đáy và a là độ dài mỗi cạnh của đáy)

h: là chiều cao của lăng trụ đều

S xq: là diện tích xung quanh của lăng trụ đều

Công thức tính diện tích xung quanh không bao gồm diện tích của các đáy, mà chỉ tập trung vào các mặt bên của hình lăng trụ và giúp chúng ta đánh giá chính xác diện tích của phần bên ngoài.

Công thức tính diện tích toàn phần

Khi làm việc với hình lăng trụ đều, một thông số không thể thiếu trong các phép toán là diện tích toàn phần, bao gồm cả diện tích các đáy và các mặt bên của lăng trụ. Dưới đây là công thức tính diện tích toàn phần của lăng trụ đều là:

S tp = S đáy x 2 + S xq

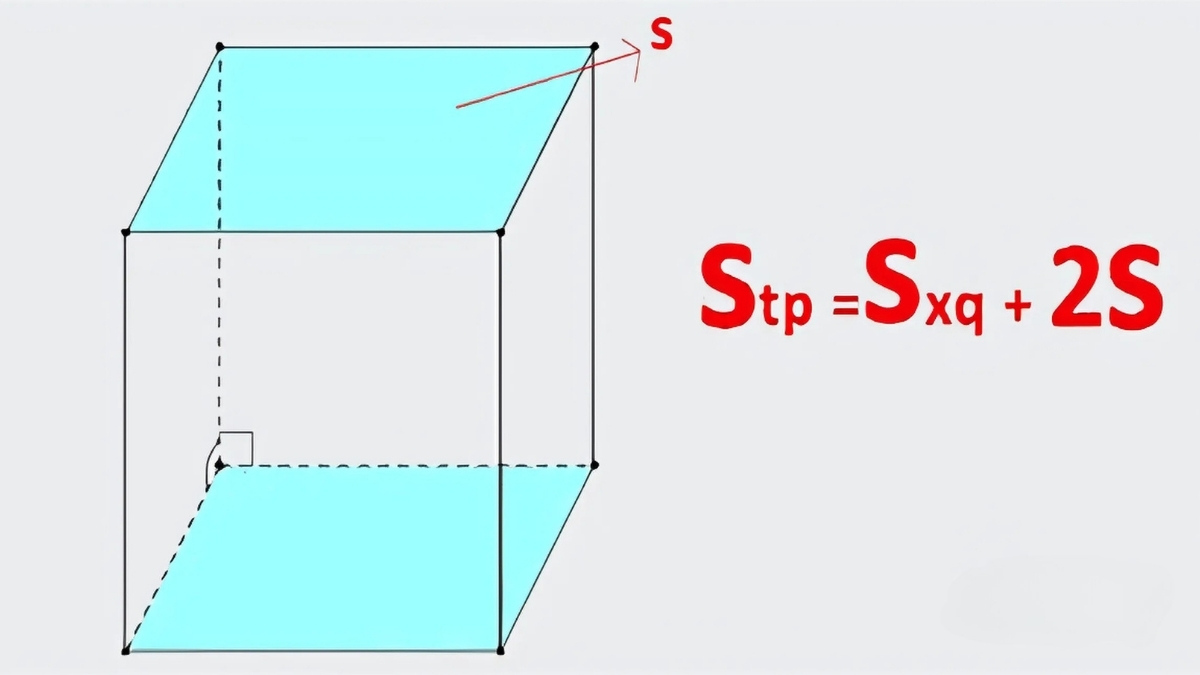
Trong đó:

S xq: là diện tích xung quanh của hình lăng trụ đều 

S đáy: là diện tích của một đáy

S tp: là diện tích toàn phần của lăng trụ đều

Công thức này giúp tính tổng diện tích của toàn bộ bề mặt lăng trụ, bao gồm cả hai đáy và các mặt bên.

Công thức tính thể tích

Dưới đây là công thức tính thể tích khối lăng trụ đều là:

V = S đáy × h

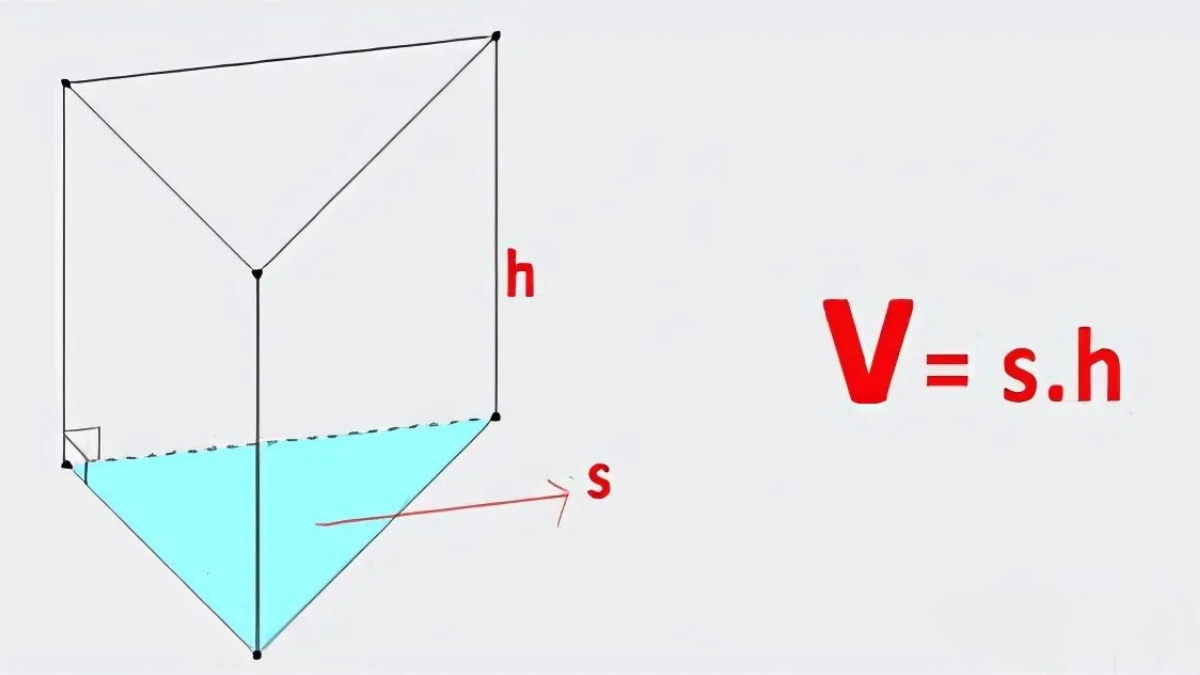
Trong đó:

h: là chiều cao của lăng trụ, tức là khoảng cách vuông góc giữa hai đáy

S đáy: là diện tích đáy

V: là thể tích của lăng trụ đều

Công thức này cho biết dung tích không gian mà lăng trụ chiếm giữ, thường được ứng dụng trong thực tế để tính thể tích các vật thể có hình dạng tương tự.

Các dạng bài tập cơ bản về hình lăng trụ đều

Bài toán 1: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật

Hãy cùng xem xét một hình hộp chữ nhật có các kích thước lần lượt là chiều dài 8 cm, chiều rộng 6 cm và chiều cao 4 cm. 

Bài giải

1. Tính diện tích xung quanh

Diện tích xung quanh của hình hộp chữ nhật được tính bằng công thức: S xq = P đáy x h

Trước tiên, ta tính chu vi của đáy hình chữ nhật: P đáy = (8 + 6) × 2 = 28 cm

Sau đó, tính diện tích xung quanh: S xq = 28 × 4 = 112 cm²

1. Tính diện tích toàn phần

Diện tích toàn phần được tính bằng công thức: S tp = S đáy x 2 + S xq

Trước tiên, ta tính diện tích một đáy: S đáy = 8 × 6 = 48 cm²

Sau đó, tính diện tích toàn phần: S tp = 112 + 2 × 48 = 208 cm²

Đáp số:

Diện tích xung quanh: 112 cm²

Diện tích toàn phần: 208 cm²

Bài toán 2: Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh bên bằng 4a, đường chéo của lăng trụ bằng 5a và bạn hãy tính thể tích của khối lăng trụ này.

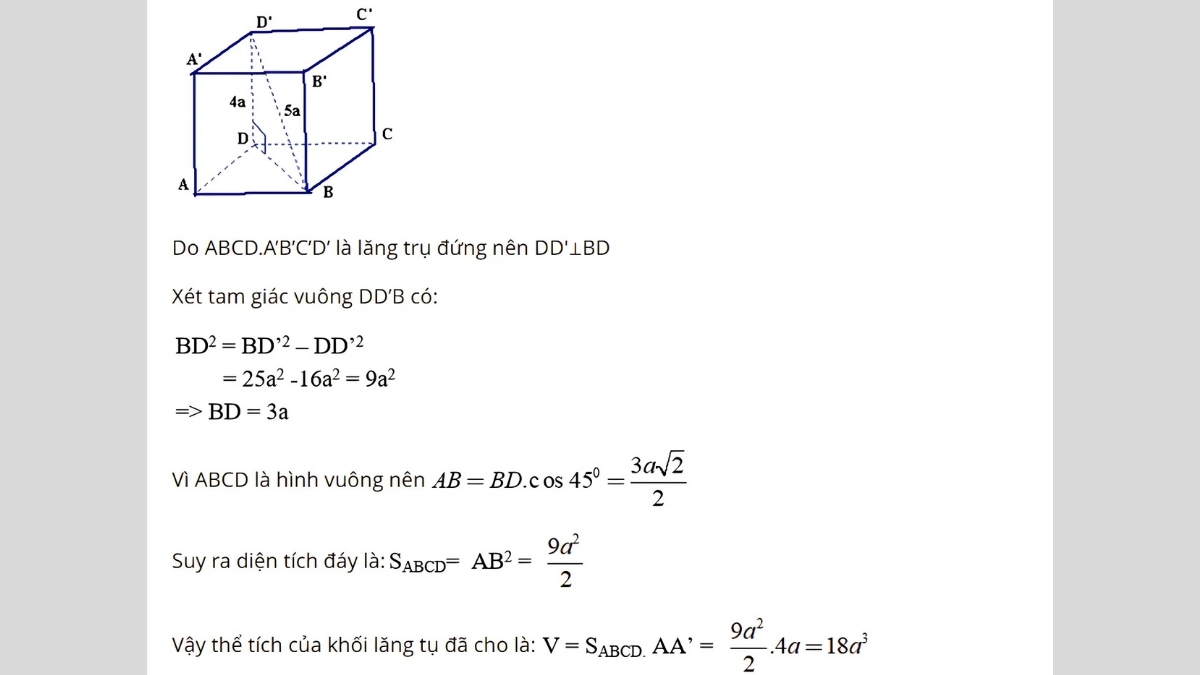
Một số câu hỏi bạn có thể quan tâm

Khi tìm hiểu về lăng trụ đều, có rất nhiều khía cạnh thú vị mà bạn có thể quan tâm. Từ những khái niệm cơ bản cho đến các công thức tính toán, mỗi bước trong quá trình tìm hiểu về lăng trụ đều mở ra những góc nhìn toàn diện về loại hình học này. Dưới đây là một số câu hỏi thường gặp liên quan đến khối lăng trụ đều, mà bạn có thể tìm hiểu qua:

Lăng trụ đứng khác gì lăng trụ đều?

Lăng trụ đứng và lăng trụ đều là hai khái niệm khác nhau trong hình học.

Lăng trụ đứng là lăng trụ có các cạnh bên vuông góc với đáy và phần đáy là bất kỳ hình đa giác nào (tam giác, tứ giác, lục giác…). Các cạnh bên của lăng trụ đều tạo thành những hình chữ nhật hoàn hảo, với độ dài đồng nhất và sự đối xứng rõ rệt.

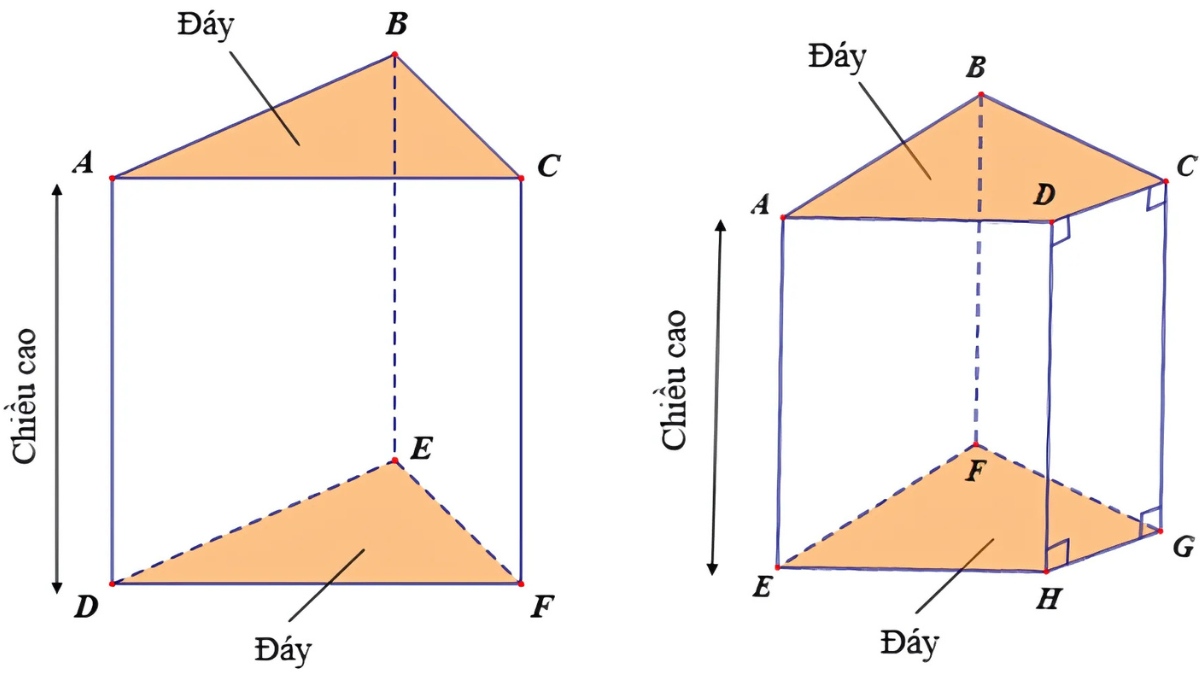
Lăng trụ đều là lăng trụ có hai đáy là hai hình đa giác đều và các cạnh bên song song, bằng nhau. Hình này có tính đối xứng cao, với đáy luôn là hình đa giác đều (tam giác đều, vuông, lục giác đều…).

Khác biệt chính là lăng trụ đứng chỉ yêu cầu cạnh bên vuông góc với đáy, không bắt buộc đáy phải là hình đa giác đều. Lăng trụ đều là một hình khối không gian đặc biệt, nổi bật với đặc điểm có đáy là một đa giác đều và các cạnh bên thì bằng nhau.

Lăng trụ tam giác, tứ giác đều có cạnh bên là hình gì?

Lăng trụ tam giác đều: Có các cạnh bên là những đoạn thẳng song song và độ dài đồng nhất. Khi quan sát từ một góc nhìn bên cạnh, các cạnh bên này tạo thành những hình chữ nhật đều, mang đến vẻ đẹp đối xứng và hài hòa.

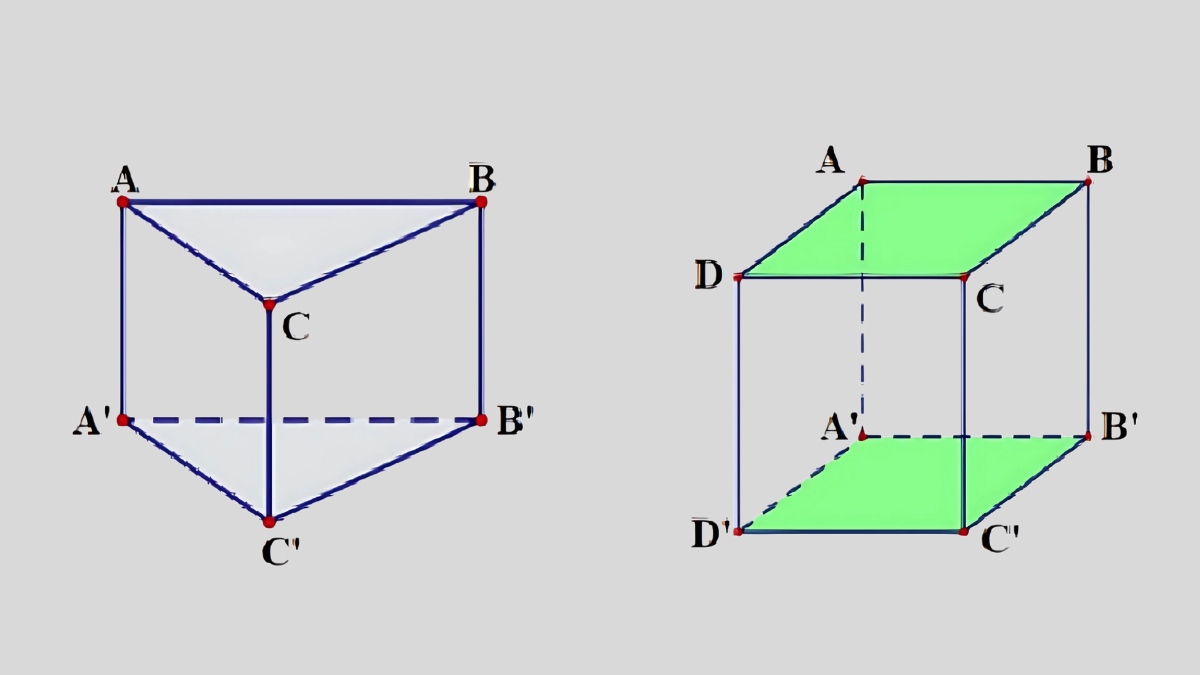
Lăng trụ tứ giác đều: Các cạnh bên của lăng trụ tứ giác đều cũng là các đoạn thẳng song song, có chiều dài bằng nhau và tạo thành các hình chữ nhật khi nhìn từ bên cạnh.

Tóm lại, chúng ta đã cùng nhau khám phá và tìm hiểu về hình lăng trụ đều, một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học không gian 3D. Lăng trụ đều không chỉ sở hữu cấu trúc đơn giản mà còn có ứng dụng đa dạng trong nhiều lĩnh vực, từ kiến trúc, cơ học đến thiết kế đồ họa. Hiểu rõ về khối lăng trụ đều giúp bạn dễ dàng áp dụng các kiến thức này vào các bài toán hình học và ứng dụng thực tế. Nếu muốn tìm hiểu thêm các kiến thức về giáo dục, bạn có thể truy cập Sforum để cập nhật thông tin mới nhất nhé!

Đọc các bài viết cùng chủ đề: Góc Học & Dạy 4.0