Công thức tính thể tích hình nón và bài tập ví dụ chi tiết

Trong chương trình toán học, công thức tính thể tích hình nón cụt là một kiến thức rất được chú trọng. Việc hiểu cách tính công thức này không chỉ giúp học sinh thành thạo việc tính toán mà còn áp dụng hiệu quả trong kỳ thi tốt nghiệp THPT. Trong nội dung sau, Sforum sẽ hướng dẫn bạn cách tính thể tích hình nón đơn giản và những bài tập ví dụ để mọi người dễ hiểu hơn nhé.

Hình nón (khối nón) là gì?

Trong lĩnh vực hình học, hình nón là một hình học khối ba chiều đặc biệt. Nó có bề mặt được uốn cong từ đáy và thu hẹp dần lên phía đỉnh. Trong đó, phần đỉnh nhọn của hình nón sẽ được gọi là đỉnh, còn bề mặt tròn phẳng ở bên dưới chính là đáy. Khi nhìn vào thực tế, chúng ta thường bắt gặp hình nón thông qua những vật dụng vô cùng quen thuộc như: Nón lá, cây kem ốc quế hay mũ sinh nhật,...

Về cơ bản, cấu trúc của hình nón bao gồm có 3 thuộc tính, bao gồm: Một đỉnh nhọn hình tam giác, một mặt đáy hình tròn và không có cạnh nào liên kết giữa đỉnh và đáy. Chiều cao của hình nón được ký hiệu là h, đây là khoảng cách vuông góc tính từ tâm của đáy tròn đến đỉnh của khối nón. Trong mặt cắt ngang của hình nón, đường cao và bán kính của đáy sẽ tạo thành một hình gọi là tam giác vuông.

Các công thức tính thể tích hình nón và ví dụ minh họa

Hình nón là một loại hình học phổ biến trong toán học nên việc tính thể tích của nó cũng là một kỹ năng cần thiết. Hiện nay, tùy thuộc vào từng loại hình nón mà chúng ta sẽ có những công thức tính khác nhau. cụ thể: 

Công thức chung tính thể tích hình nón

Cách tính thể tích hình nón chung sẽ sử dụng một công thức áp dụng cho mọi loại hình nón khác nhau với chiều cao và diện tích đáy cho trước. Theo đó, để tính được thể tích hình nón chung thì chúng ta có công thức dưới đây:

V = ⅓π x R² x h

Trong đó:

• V: Thể tích hình nón
• π: ≈ 3,14
• r: Bán kính
• h: Chiều cao

Ví dụ: Nếu hình nón có r = 3cm (bán kính đáy) và h = 5cm (chiều cao) thì cách tính thể tích hình nón sẽ được áp dụng như sau:

V = 1/3π × 3² × 5 = 15π ≈ 47.12cm³

Để hỗ trợ việc tính toán đảm bảo chính xác, việc đầu tư một chiếc máy tính cầm tay chất lượng rất quan trọng. Tuy nhiên, để tránh mua nhầm hàng giả thì bạn hãy ưu tiên đến CellphoneS để đảm bảo mua hàng chính hãng. Nếu chưa biết nên mua mẫu nào, hãy để Sforum gợi ý những sản phẩm sau:

[Product_Listing categoryid="1661" propertyid="" customlink="https://cellphones.com.vn/may-tinh-cam-tay.html" title="Các sản phẩm máy tính cầm tay đang được quan tâm nhiều tại CellphoneS"]

Công thức tính thể tích hình nón tròn xoay

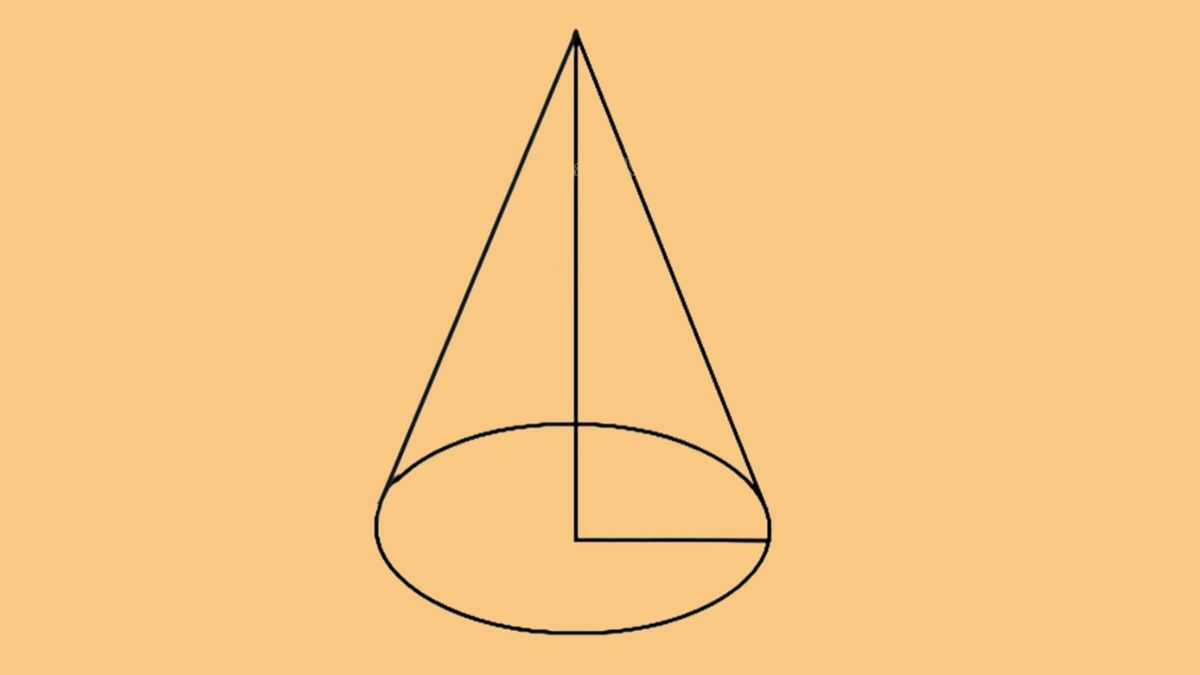
Hình nón tròn xoay có đường thẳng nối từ đỉnh đến tâm của mặt đáy hình tròn và vuông góc với mặt đáy. Cách tính thể tích hình nón tròn xoay cũng khá đơn giản dựa theo công thức sau:

V = ⅓ x B x h = 1/3π x R² x h

Trong đó:

• V: Thể tích khối nón
• π: ≈ 3.14159
• R: Bán kính đáy của nón
• h: Chiều cao của nón
• B: Diện tích đáy

Ví dụ: Một hình nón có R = 6cm (bán kính đáy) và h = 10cm (chiều cao). Khi đã biết bán kính của hình nón, bạn cần tính diện tích đáy theo công thức B = π.r² = π × 6² = 36π. Lúc này, khi áp dụng vào công thức thì chúng ta sẽ có cách tính thể tích như sau:

V = ⅓ × 36π × 10 = 120π ≈ 376.991cm³

Công thức tính thể tích hình nón cụt

Hình nón cụt là hình được cắt ngang và chia thành hai đáy với hai bán kính hoàn toàn khác biệt. Với cách tính thể tích hình nón cụt, các bạn cần dựa vào công thức:

V = 1/3π x h x (r1² + r1 x r2+ r2²)

Trong đó:

• V: Thể tích hình nón cụt

• r1, r2: Hai bán kính mặt đáy của khối nón cụt
• h: Chiều cao nối hai đáy hình nón
• π: ≈ 3.14159

Ví dụ: Cho một hình nón cụt có r2 = 9cm (bán kính đáy lớn), r1 = 5cm (bán kính đáy nhỏ) và chiều cao nối giữa hai đáy là h = 8cm. Theo đó, áp dụng công thức tính thể tích hình nón cụt thì ta sẽ có: V = 1/3π x 8 x (5² + 5 x 9 + 9²) ≈ 1264,37cm³.

Cách xác định đường sinh, đường cao và bán kính đáy

Trong hình nón, đường cao h là đoạn thẳng vuông góc từ đỉnh nón đến tâm của mặt đáy. Đường sinh l là khoảng cách bắt đầu từ một vị trí trên đường tròn đáy đến đỉnh. Khi đó, các thành phần của tam giác gồm có:

• r (bán kính đáy) và h (đường cao) thuộc hai cạnh góc vuông của hình tam giác.
• l (đường sinh) là cạnh huyền tam giác.

Khi biết r (bán kính đáy) và h (đường cao), ta sẽ tính l (đường sinh) bằng định lý Pythagore như sau: l= √r² + h².

Nếu biết r (bán kính đáy) và l (đường sinh), ta có thể tính được h (đường cao) bằng công thức: h= √l² - r².

Tiếp tục, Nếu biết đường cao h và đường sinh l, ta có thể tính được bán kính đáy r bằng công thức: r= √l² - h².

Một số dạng bài tập tính thể tích hình nón

Khi đã hiểu rõ công thức tính thể tích của hình nón, bạn có thể thực hành một số dạng bài tập để áp dụng các công thức trên một cách nhuần nhuyễn. Trong đó, một số dạng bài tập tính thể tích hình nón phổ biến gồm có:

Bài tập 1

Đề bài: Cho một khối nón có l (độ dài đường sinh) = 5cm và r (bán kính đáy) = 3cm, hãy tính thể tích khối nón này?

Lời giải: Để tính thể tích khối nón, ta cần chiều cao h của nón dựa theo công thức: h= √l² - r² = √5² - 3² = √16 = 4cm.

Thay số vào công thức tính thể tích: V = ⅓π x R² x h, ta sẽ có:

V = ⅓π x 3² x 4 = ⅓π x 9 x 4 = 12πcm³ ≈ 37.699cm³.

Bài tập 2

Đề bài: Một hình nón có r (bán kính đáy) = 4cm và h (đường cao) = 9cm, hãy tính thể tích hình nón này?

Lời giải: Trong bài tập này, bạn tiếp tục áp dụng công thức tính thể tích hình nón: V = ⅓π x R² x h. Từ đây, ta sẽ có cách tính như sau: V = ⅓π x 4² x 9 = 48π ≈ 150.8cm³.

Bài tập 3

Đề bài: Một hình chóp cụt có hai mặt đáy với đường kính lần lượt là 12cm và 18cm, chiều cao nối liền giữa hai mặt đáy là 15cm. Hãy tính thể tích của khối chóp cụt?

Lời giải: Để tính thể tích của khối nón cụt theo công thức V = 1/3π x h x (r1² + r1 x r2+ r2²), ta cần biết bán kính R dựa trên cách tính sau:

• r1 (Bán kính đáy lớn) = 18:2 = 9cm
• r2 (Bán kính đáy nhỏ) = 12:2 =6 cm

Khi đã có bán kính, bạn tiến hành thay số vào công thức tính khối nón cụt như sau: V = 1/3π x 15 x (9² + 9 x 6+ 6²) = 855πcm³ ≈ 2685.84cm³.

Để thuận tiện trong việc học, làm bài tập và tra cứu cách tính thể tích hình non, bạn có thể tham khảo nhiều dòng điện thoại chính hãng tại CellphoneS. Với vô vàn lựa chọn hấp dẫn, giá hợp lý, các sản phẩm sau đây sẽ là công cụ đắc lực hỗ trợ bạn học tập tốt hơn:

[Product_Listing categoryid="3" propertyid="" customlink="https://cellphones.com.vn/mobile.html" title="Danh sách điện thoại đang được quan tâm nhiều tại CellphoneS"]

Trên đây là công thức tính thể tích hình nón cụt và các bài tập ví dụ dễ hiểu mà Sforum muốn chia sẻ đến bạn. Hy vọng thông qua bài viết này, các bạn sẽ biết cách tính thể tích hình nón đơn giản để thành thục hơn khi tính toán và hỗ trợ trong kỳ thi tốt nghiệp THPT quan trọng. Nếu bạn muốn tham khảo thêm nhiều bài toán thú vị hoặc các thông tin giáo dục khác, hãy truy cập Sforum để tìm hiểu nhé.

Xem thêm bài viết ở chuyên mục: Mẹo vặt