Tổng hợp công thức và bài tập tính thể tích khối lăng trụ

Trong hình học không gian, thể tích khối lăng trụ lục giác đều là một chủ đề quan trọng với nhiều bài toán thú vị. Đặc biệt, việc nắm vững các công thức thể tích khối lăng trụ đứng sẽ giúp giải quyết các bài tập nhanh chóng và hiểu sâu hơn về các khái niệm hình học. Bài viết này tổng hợp thêm bài tập minh họa, giúp áp dụng lý thuyết một cách dễ dàng và chính xác.
Lý thuyết về thể tích khối lăng trụ
Khối lăng trụ là dạng hình học trong không gian có hai đáy đối xứng và giống hệt nhau, được kết nối bởi các mặt phẳng bao quanh. Đặc biệt, những mặt bao quanh này thường có dạng hình chữ nhật hoặc hình bình hành.

Để tính thể tích khối lăng trụ, bạn chỉ cần lấy diện tích của một mặt đáy nhân với chiều cao - khoảng cách vuông góc giữa hai đáy. Công thức này đơn giản nhưng rất quan trọng, giúp ta xác định được dung lượng không gian mà khối lăng trụ chiếm trong thực tế.
Các bạn học sinh nếu đang tìm kiếm một công cụ học tập đa năng, iPad chính là lựa chọn hoàn hảo. Tương thích với nhiều ứng dụng học tập, iPad giúp bạn dễ dàng ghi chú, học online và giải trí sau giờ học. Tham khảo các mẫu sản phẩm đang được yêu thích giúp quá trình làm bài trở nên thú vị và sáng tạo hơn nhé!
[Product_Listing categoryid="944" propertyid="" customlink="https://cellphones.com.vn/tablet/ipad.html" title="Các mẫu iPad đang được quan tâm nhiều tại CellphoneS"]
Công thức thể tích khối lăng trụ
Công thức thể tích khối lăng trụ có đáy diện tích S và chiều cao (tức khoảng cách vuông góc giữa hai mặt đáy) h là: V=S.h. Tiếp theo đây, ta sẽ đi tìm hiểu cách tính thể tích khối lăng trụ cho những trường hợp cụ thể và một số ví dụ minh hoạ đơn giản nhé!
Thể tích hình lăng trụ đứng
Ở lăng trụ đứng, các mặt bao quanh là các hình chữ nhật nằm vuông góc với mặt phẳng đáy, còn đáy thường có dạng đa giác. Độ cao của lăng trụ đứng được xác định bằng độ dài cạnh bên.

Ví dụ, xét lăng trụ đứng có đáy chữ nhật với kích thước chiều dài 4 cm, chiều rộng 3 cm, và cạnh bên dài 5,5 cm. Thể tích khối lăng trụ đứng là: V = S × h = 4 × 3 × 5,5 = 12 × 5,5 = 66 cm³.
Khối lăng trụ đều, đáy là một hình đa giác đều
Khối lăng trụ đều có đặc điểm là mặt đáy là một hình đa giác đều, như hình tam giác đều, vuông, lục giác đều,... Các mặt bao quanh của khối này có dạng hình chữ nhật và vuông góc với phần đáy.
Ví dụ: Diện tích đáy của hình lục giác đều cạnh dài 4 cm và chiều cao 8 cm được tính bằng công thức: S= 332a2 =33242=243 (cm2) (a là độ dài cạnh lục giác đều). Thể tích khối lăng trụ lục giác đều này sẽ là: S=Sđáyh=2438=1923 (cm3)
Thể tích khối lăng trụ chữ nhật
Nếu cách tính thể tích khối lăng trụ lục giác đều có hơi phức tạp thì lăng trụ chữ nhật sẽ đơn giản hơn. Công thức tính là: V = l × w × h. Trong đó, l là chiều dài đáy, w là chiều rộng đáy, còn h là chiều cao của khối lăng trụ. Ví dụ: Thể tích khối lăng trụ chữ nhật có chiều dài 5 cm, chiều rộng 3 cm và chiều cao 10 cm là: V = 5 × 3 × 10 = 150 cm³.

Thể tích khối lập phương
Khối lập phương là một hình học không gian đặc biệt thuộc nhóm lăng trụ chữ nhật, được tạo thành khi tất cả các cạnh của nó có cùng độ dài. Để xác định thể tích của khối lập phương, ta áp dụng công thức V = a³, với a là chiều dài của một cạnh. Ví dụ: Thể tích khối lập phương có cạnh dài 6 cm là: V = 6³ = 216 cm³.
Tổng hợp các bài tập tính thể tích hình lăng trụ (Kèm lời giải)
Để giúp các bạn học sinh củng cố kiến thức về thể tích hình lăng trụ, dưới đây là một số bài tập trắc nghiệm và tự luận, kèm theo lời giải chi tiết. Những bài tập này sẽ hỗ trợ bạn hiểu và thành thạo trong việc áp dụng công thức tính thể tích vào nhiều tình huống khác nhau.
Bài tập trắc nghiệm
Câu 1: Xét một khối lăng trụ đứng có phần đáy là hình vuông với độ dài cạnh là 4 cm và chiều cao của khối là 10 cm. Thể tích khối lăng trụ là:
- 160 cm³
B. 140 cm³
C. 120 cm³
D. 100 cm³
Lời giải:
Diện tích đáy = 4 × 4 = 16 cm²
Thể tích = diện tích đáy × chiều cao = 16 × 10 = 160 cm³
Vậy chọn A. 160 cm³.
Bài 2: Cho lăng trụ tam giác đều ABC.A′B′C′, cạnh đáy bằng 4, góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60 độ . Tính chiều cao A′A.
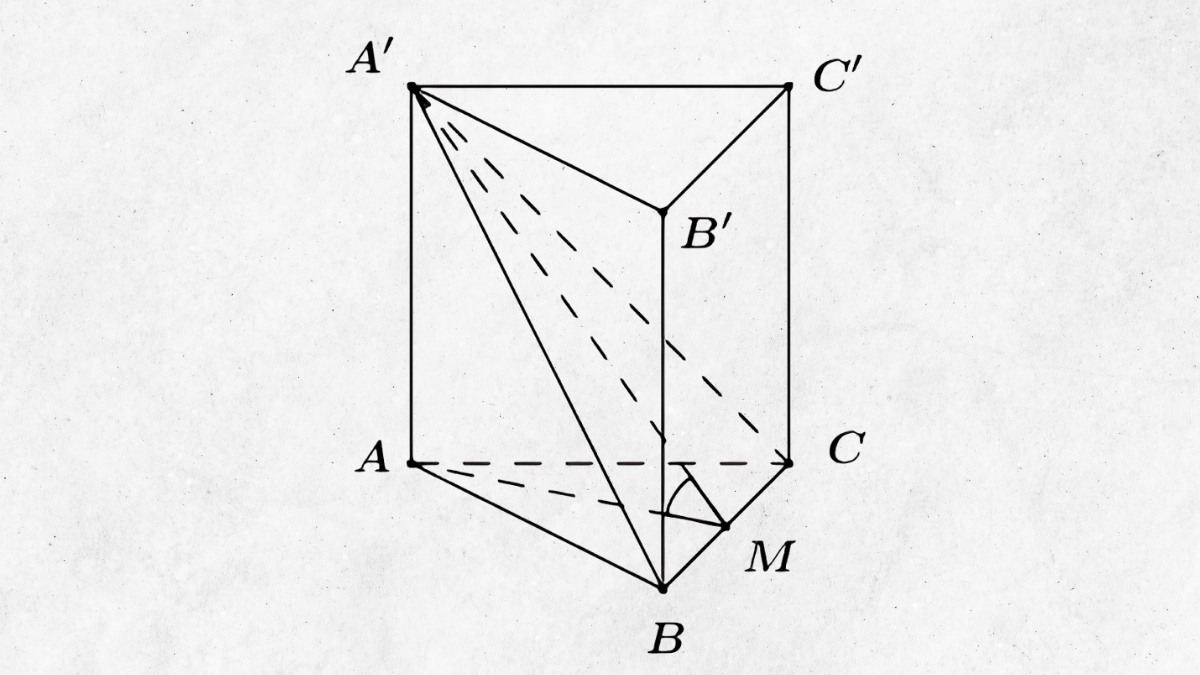
- 23
- 6
- 43
- 4
Lời giải:
Góc giữa mặt phẳng (A′BC) và (ABC) là 60 độ và đáy tam giác đều cạnh 4, ta có đường cao AM=432=23. Trong tam giác vuông A′MA: tan 600=A'AAM. Vậy chiều cao A’A là:A'A = tan 600AM=233 = 6.
Vậy chọn đáp án B.
Bài tập tự luận
Bài 1: Xem xét một hình lăng trụ đứng với đáy hình chữ nhật, biết rằng chiều rộng 5 cm, chiều dài 7 cm và chiều cao 12 cm. Tính thể tích của khối lăng trụ.
Lời giải:
Diện tích đáy = 5 × 7 = 35 cm²
Thể tích = diện tích đáy × chiều cao = 35 × 12 = 420 cm³
Vậy thể tích khối lăng trụ là 420 cm³.
Bài 2: Xét hình lăng trụ ABC.A′B′C′ có đáy là một tam giác đều với cạnh dài a. Hình chiếu vuông góc của điểm A' xuống mặt phẳng (ABC) nằm tại vị trí trọng tâm của tam giác ABC, và góc giữa đường thẳng AA' với mặt phẳng đáy (ABC) bằng 30 độ. Tìm thể tích khối lăng trụ ABC.A′B′C′.

Lời giải:
Đặt H làm trọng tâm tam giác đều ABC, tiếp tục lấy M ở điểm chính giữa cạnh BC.
Ta có: AH = 23AM=23a32=a33
Khi đó A'H= HAtan300 = a3. Vậy suy ra diện tích đáy ABC là: S=a234
Vậy thể tích khối lăng trụ là: VABC.A'B'C'=SABCA'H=a234a3=a3312
Khi đã biết công thức thể tích khối lăng trụ đứng, các bạn học sinh cần lưu ý áp dụng đúng và hiệu quả. Hy vọng qua bài viết, các bạn sẽ dễ dàng giải được các bài toán liên quan đến thể tích khối lăng trụ lục giác đều. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng của mình, từ đó tự tin hơn trong việc giải quyết các bài toán không gian.








Bình luận (0)