Bất đẳng thức Cô si (Cauchy) là gì? Bài tập ví dụ minh họa

Bất đẳng thức Cô si (Cauchy) là một nguyên lý quan trọng trong toán học, đóng vai trò nền tảng trong nhiều bài toán liên quan đến bất đẳng thức. Nhờ tính ứng dụng rộng rãi, nó không chỉ xuất hiện trong các kỳ thi mà còn là công cụ mạnh mẽ để đánh giá giới hạn của biểu thức. Hãy cùng Sforum đi vào định nghĩa cụ thể và các ví dụ minh họa cụ thế sau đây.

Bất đẳng thức Cô si là gì?

Bất đẳng thức Cô si là một nguyên lý toán học quan trọng trong lĩnh vực đại số và bất đẳng thức, khẳng định mối quan hệ giữa trung bình cộng và trung bình nhân của một tập hợp số không âm. Cụ thể, với hai số thực không âm a và b, ta luôn có:

Với dấu “=” chỉ xảy ra khi và chỉ khi a=b

Điều này có nghĩa là trung bình cộng không bao giờ nhỏ hơn trung bình nhân, và hai giá trị này chỉ bằng nhau khi tất cả các số trong tập hợp bằng nhau. Bất đẳng thức này đóng vai trò nền tảng trong nhiều bài toán toán học, đặc biệt là trong việc chứng minh các bất đẳng thức phức tạp.

Ngoài bài tập bất đẳng thức Cô si, bạn cũng cần rèn luyện thêm nhiều trọng điểm kiến thức khác. Hãy rèn luyện thêm càng bài tập thú vị khác chỉ chỉ với chiếc laptop cấu hình tiêu chuẩn với giá ưu đãi sau.

[Product_Listing categoryid="1054" propertyid="" customlink="https://cellphones.com.vn/laptop/sinh-vien.html" title="Tham khảo danh sách laptop sinh viên được quan tâm tại CellphoneS!"]

Các dạng biểu diễn bất đẳng thức Cô si

Bất đẳng thức Cô si là một trong những nguyên lý quan trọng giúp so sánh các giá trị trung bình trong toán học. Dưới đây là một số cách thể hiện phổ biến của bất đẳng thức Cauchy (Cô si):

Không chỉ giới hạn trong các bài toán bất đẳng thức, bất đẳng thức Cosi còn xuất hiện rộng rãi trong nhiều lĩnh vực như hình học, đại số và phân tích. Tùy vào ngữ cảnh áp dụng, bất đẳng thức này có thể được biểu diễn dưới nhiều dạng khác nhau, mỗi dạng đều có ý nghĩa và ứng dụng riêng.

Chứng minh bất đẳng thức Cô si

Chứng minh bất đẳng thức Cô si không chỉ giúp khẳng định tính đúng đắn của nó mà còn mở ra nhiều hướng tiếp cận trong việc xử lý các bài toán bất đẳng thức phức tạp. Có nhiều phương pháp khác nhau để chứng minh, từ cách tiếp cận đại số đơn giản đến các lập luận hình học trực quan.

Chứng minh bất đẳng thức Cosi với 2 số thực không âm

Bài tập bất đẳng thức Cô si chứng minh với 2 số thực không âm là dạng tương đối quen thuộc về các hướng thực hiện lẫn tính ứng dụng. 

• Phương hướng chứng minh: Biến đổi biểu thức về dạng bình phương để tận dụng tính chất không âm của bình phương số thực.
• Gợi ý thực hiện:

Như vậy, chúng ta đã chứng minh bất đẳng thức Cô si trong trường hợp hai số thực không âm bằng cách sử dụng phép biến đổi bình phương. Qua đó khẳng định sự đúng đắn và tính ứng dụng của nguyên lý này trong nhiều bài toán toán học khác.

Chứng minh bất đẳng thức Cosi với 3 số thực không âm

Bất đẳng thức Cô si còn có thể ứng dụng cho trường hợp tăng thêm 1 số thực không âm so với đẳng thức gốc. Việc chứng minh cho trường hợp ba số giúp khẳng định tính đúng đắn của bất đẳng thức trong phạm vi rộng hơn, đồng thời tạo nền tảng cho các bài toán liên quan đến bất đẳng thức và tối ưu hóa.

• Phương hướng: Vận dụng phương pháp quy nạp hoặc sử dụng tính chất của bất đẳng thức Cô si đã chứng minh cho hai số. Cách tiếp cận hợp lý nhất là áp dụng bất đẳng thức Cô si hai số theo từng bước để suy ra kết quả mong muốn.
• Gợi ý cách thực hiện:

Như vậy, chúng ta đã chứng minh bất đẳng thức Cauchy trong trường hợp ba số thực không âm bằng cách mở rộng từ trường hợp hai số. Nhờ đó, bạn có thể vận dụng nhanh công thức để làm nhanh các bài tập khác nhất là trong bài thi trắc nghiệm.

Chứng minh bất đẳng thức Cosi với n số thực không âm

Bất đẳng thức Cô si không chỉ áp dụng cho một số lượng nhỏ các số mà còn mở rộng cho một tập hợp lớn hơn. Việc chứng minh tổng quát cho n số thực không âm giúp khẳng định quy luật giữa trung bình cộng và trung bình nhân trong trường hợp tổng quát.

• Phương hướng: Để chứng minh bất đẳng thức này, ta có thể sử dụng quy nạp toán học, một phương pháp hữu ích để mở rộng từ trường hợp nhỏ lên trường hợp tổng quát.
  • Bước đầu: Kiểm tra tính đúng đắn của bất đẳng thức khi n=2 và n=3 để tạo cơ sở.
  • Bước quy nạp: Giả sử bất đẳng thức đúng với n số, ta chứng minh rằng nó cũng đúng với n+1 số.
• Gợi ý chứng minh bất đẳng thức Cô si với n số thực không âm

Vì bất đẳng thức đúng với n=2 và có tính kế thừa qua bước quy nạp, theo nguyên lý quy nạp toán học, ta kết luận rằng bất đẳng thức Cô si đúng với mọi số nguyên n≥2. Kết quả chứng minh bất đẳng thức Cô si có nhiều ứng dụng quan trọng trong giải toán bất đẳng thức, tối ưu hóa, và phân tích dữ liệu.

Bài tập về bất đẳng thức Cô si

Bài tập bất đẳng thức Cô si là một phần quan trọng trong việc giải nhanh các đề toán liên quan đến bất đẳng thức, nhất là ở dạng câu hỏi trắc nghiệm. Hãy áp dụng ngay vào từng trường hợp cụ thể thông qua các bài tập thường gặp sau đây.

Sử dụng bất đẳng thức Cô si để tìm min/max cơ bản

Đề bài mẫu: Cho hai số thực không âm a,b thỏa mãn a+b=10. Tìm giá trị lớn nhất của tích =a⋅b. 

• Hướng giải quyết: Bất đẳng thức Cô si có thể được áp dụng để tìm giới hạn trên của tích hai số khi biết tổng của chúng.
• Gợi ý giải bài tập bất đẳng thức Cô si:

Áp dụng bất đẳng thức Cô si cho hai số a,b:

Bình phương hai vế ta được : 

Dấu "=" xảy ra khi a=b, tức là a=b=5. Vậy giá trị lớn nhất của P là 25, đạt được khi a=b=5.

Sử dụng bất đẳng thức Cô si để tìm min/max nâng cao

Đề bài: Cho ba số thực không âm x,y,z thỏa mãn x+y+z=12. Tìm giá trị nhỏ nhất của tổng nghịch đảo:

• Hướng giải: Ta sẽ sử dụng bất đẳng thức Cô si dạng nghịch đảo để thiết lập giới hạn dưới cho biểu thức S.
• Gợi ý cách làm bài tập bất đẳng thức Cô si tìm max/min:

Áp dụng bất đẳng thức Cô si cho ba số dương:

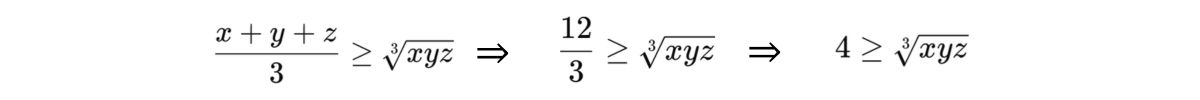
Dấu bằng xảy ra khi x=y=z

Bình phương và nhân cả hai vế, ta có:

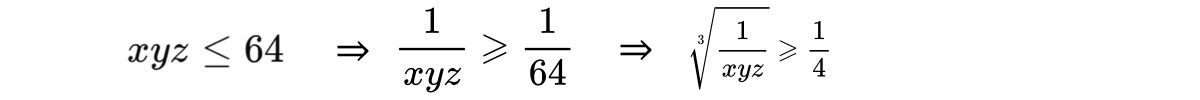
Dấu bằng xảy ra khi x=y=z

Bất đẳng thức Cô si cho S ta có:

Vậy giá trị nhỏ nhất của S là ¾ , khi x=y=z=4

Bất đẳng thức Cô si (Cauchy) là một công cụ quan trọng giúp giải quyết nhiều bài toán liên quan đến cực trị và so sánh giá trị của biểu thức. Việc nắm vững nguyên tắc và cách áp dụng không chỉ giúp rèn luyện tư duy toán học mà còn mở ra nhiều hướng tiếp cận sáng tạo trong giải toán. Đừng quên tham khảo thêm các chủ điểm về giáo dục và bài tập khác trên Sforum nhé.

Xem thêm bài viết trong chuyên mục: Góc Học & Dạy 4.0