Hàm hợp là gì? Cách tìm cực trị của hàm hợp

Trong toán học, hàm hợp và các bài toán về tìm cực trị khá phổ biến trên bài thi. Trong đó, dạng bài tìm cực trị hàm hợp là phổ biến nhất với mức độ bài toán đa dạng từ dễ đến khó. Để giúp các bạn học sinh hiểu rõ hơn về dạng bài tập này. Hãy cùng Sforum khám phá định nghĩa và cách tìm cực trị hàm hợp trong nội dung bài viết này nhé.

Hàm hợp là gì?

Hàm hợp là một phép toán nhận hai hàm số f và g, cho ra hàm số h với h(x) = g(f(x)). Trong phép toán này, hàm số f: X → Y và g: Y → Z được nhóm lại tạo thành một hàm mới. Sau khi hợp lại, ta biến x thuộc tập hợp X thành g(f(x)) thuộc tập hợp Z.

Ký hiệu hàm hợp: g ∘ f: X → Z. Và được định nghĩa bởi (g ∘ f )(x) =g(f(x)), với mọi x thuộcX, đọc là “g của f”, “g hợp f” hoặc “g tròn f”.

Tuy nhiên, với hàm hợp liên tục trên đoạn hay khoảng từ giá trị a đến b, thì đều tồn tại nguyên hàm của hàm số đó trên đoạn/khoảng từ a đến b nêu trên.

Để dễ hiểu hơn, bạn có thể xem ví dụ minh họa sau:

Chẳng hạn, cho f: R → R và g: R → R, trong đó:

f(x) = 2x + 6 và g(x) = 5x

• Nếu f hợp g, thì: (f ∘ g)(x) = f(g(x)) = f(5x) = 2(5x) + 6 = 10x + 6
• Nếu g hợp f, thì: (g ∘ f)(x) = g(f(x)) = g(2x + 6) = 5(2x + 6) = 10x + 30

Cách tìm cực trị hàm hợp? Ví dụ minh họa

Để tìm cực trị của hàm hợp, bạn cần biết cách tính đạo hàm hàm hợp. Cụ thể cần nắm được công thức và tính chất sau:

Thứ nhất: đạo hàm của hàm hợp: [f(g(x))]' = g'(x).f'(g(x)).

Thứ hai: tính chất đổi dấu của biểu thức:

Giải thích: Nếu x = a là nghiệm của phương trình f(x) = 0 thì có hai trường hợp sau:

• Nếu x = a là nghiệm đơn hoặc nghiệm bội bậc lẻ (ví dụ, x là nghiệm của (x - a), (x - a)³, …), thì hàm số f đổi dấu khi đi qua a.
• Nếu x = a là nghiệm bội bậc chẵn (ví dụ, x là nghiệm của (x - a)², (x - a)⁴,…), thì hàm số f không đổi dấu khi đi qua a.

Phương pháp giải bài toán tìm cực trị hàm hợp

Cách tìm cực trị của hàm hợp sẽ đi qua 3 bước. Với phương pháp này bạn có thể áp dụng với nhiều bài tập số khác nhau. Cụ thể các bước như sau:

Để tìm cực trị của hàm số y = f(g(x)) ta làm như sau:

Bước 1: Tính đạo hàm của hàm hợp [f(g(x))]'.

Bước 2: Giải phương trình [f(g(x))]' = 0.

Bước 3: Lập bảng biến thiên của hàm số và kết luận các điểm cực trị (cực đại, cực tiểu).

Bước 4:Kết luận về các điểm cực trị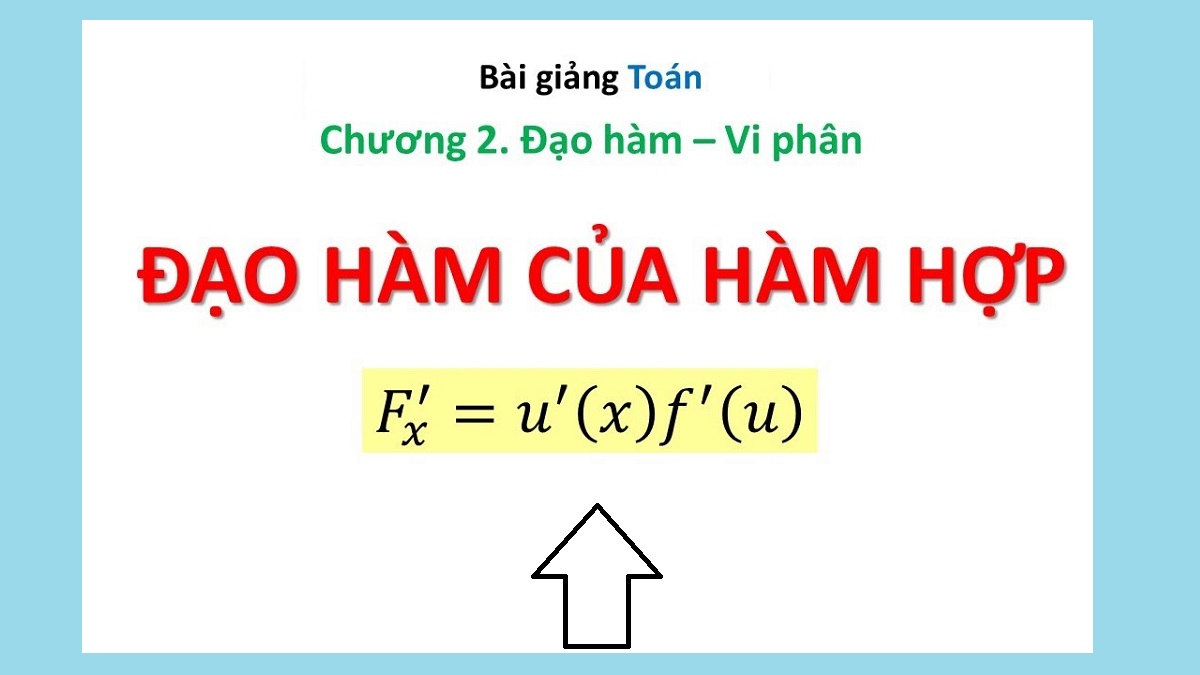

Ví dụ về hàm hợp và minh họa cách tìm cực trị

Ví dụ sau đây sẽ giúp bạn hiểu rõ hơn về phương pháp tính đạo hàm của hàm hợp.

Ví dụ: Cho hàm số y = f(x) có đạo hàm trên R và bảng xét dấu của y = f'(x) như hình bên dưới. Hãy cho biết hàm số g(x) = f (x² - 2x) có bao nhiêu điểm cực tiểu và đó là những điểm nào?

Sau đây là cách giải từng bước chi tiết:

Bước 1: Tính đạo hàm của hàm hợp g'(x). Áp dụng công thức tính đọa hàm nêu trên ta có được'

g'(x) = (x² - 2x)' f'(x² - 2x) = (2x - 2) f'(x² - 2x)

Bước 2: Giải phương trình g'(x) = (2x - 2) f'(x2 - 2x) = 0

g'(x) = 0 → (2x - 2) = 0 (1) hoặc f'(x2 - 2x) = 0 (2)

• (1): (2x - 2) = 0 → x = 1 (nghiệm đơn)
• (2): Dựa vào bảng biến thiên, f'(x² - 2x) = 0 khi:

hoặc x² - 2x = -2 → phương trình này vô nghiệm (không có nghiệm), hoặc x² - 2x = 1 → x = 1√2 (nghiệm bội bậc chẵn), hoặc x² - 2x = 3 → x = - 1 hoặc x = 3 (nghiệm đơn)

Bước 3: Xây dựng bảng biến thiên để xác định điểm cực trị như sau.

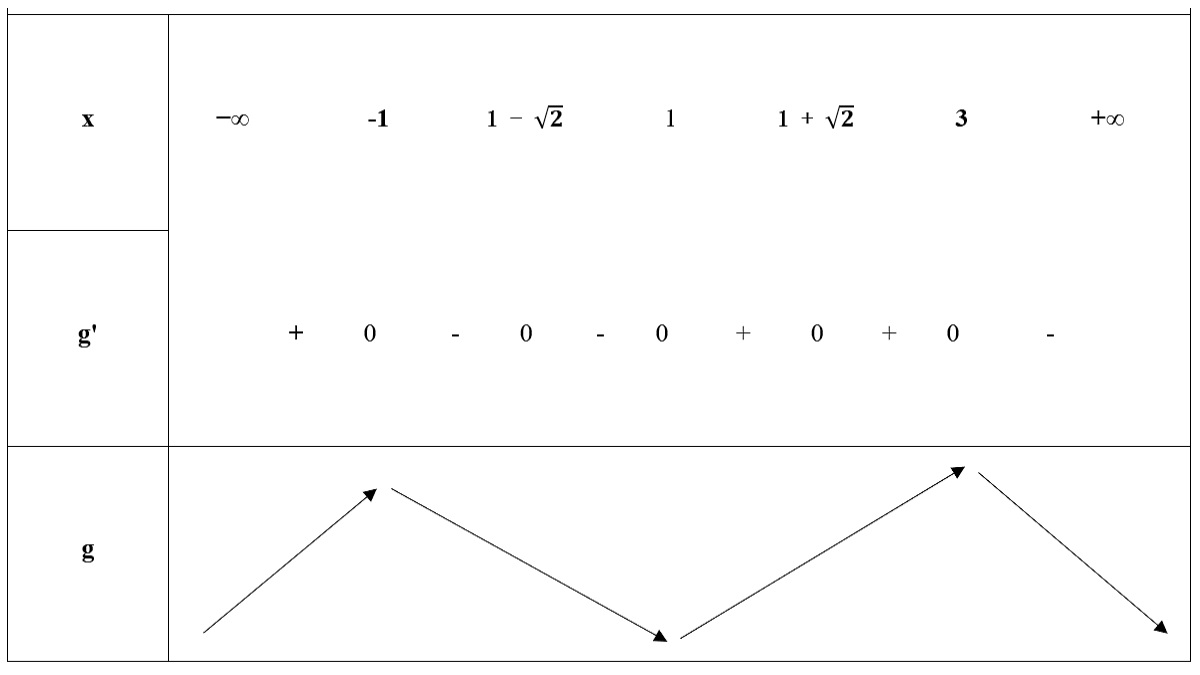
Bước 4: Kết luận: nhìn vào bảng biến thiên ta thấy, hàm số có một cực tiểu, tại điểm x = 1

Bài viết này đã giúp bạn hiểu được cách tìm cực trị và hàm hợp là gì. Hy vọng những thông tin trên sẽ giúp ích cho bạn, để lại bình luận nếu có thắc mắc nào nhé. Hãy theo dõi Sforum để cập nhật những kiến thức bổ ích nhất.