Hình chóp tứ giác là gì? Các công thức và bài tập ví dụ

Hình chóp tứ giác là một khối đa diện quen thuộc, xuất hiện nhiều trong toán học và thực tiễn. Với cấu trúc đặc biệt, hình chóp này sở hữu nhiều tính chất thú vị về phương diện hình học. Bài viết sau của Sforum sẽ giúp bạn khám phá tất tần tật thông tin về số cạnh, thể tích của hình chóp tứ giác ABCD, hãy xem ngay!

Định nghĩa hình chóp tứ giác

Hình chóp tứ giác là một khối đa diện trong không gian. Nó có mặt đáy là một tứ giác bất kỳ và bốn mặt bên là những tam giác có cùng 1 đỉnh. Các đoạn thẳng nối đỉnh này với các đỉnh của đáy được gọi là cạnh bên. 

Đường cao của hình này được xác định bằng cách nối đỉnh và hình chiếu của đỉnh đó xuống mặt đáy. Bên cạnh các bài toán về thể tích và hình khối, hình này còn được ứng dụng trong các thiết kế công trình kiến trúc và sáng tạo nghệ thuật.

Bạn đang tìm một trợ thủ đắc lực để khám phá thế giới hình học một cách dễ dàng và trực quan? Một chiếc iPad thông minh sẽ giúp bạn ghi chú nhanh chóng, vẽ hình sắc nét và học tập hiệu quả hơn bao giờ hết. Đến ngay CellphoneS để lựa chọn thiết bị phù hợp với nhu cầu của bạn với mức giá hấp dẫn nhất. Tìm hiểu ngay!

[Product_Listing categoryid="944" propertyid="" customlink="https://cellphones.com.vn/tablet/ipad.html" title="Các mẫu iPad đang được quan tâm nhiều tại CellphoneS"]

Tính chất của hình chóp tứ giác

Trước khi tìm hiểu về công thức tính diện tích, thể tích hình chóp tứ giác ABCD cũng như những bài tập vận dụng liên quan, bạn cần nắm rõ tính chất của hình này. Dưới đây là một số điểm nhận diện cơ bản giúp bạn nhanh chóng xác định hình này:

• Một chóp tứ giác sở hữu 5 mặt với mặt đáy là tứ giác bất kỳ còn mặt bên là các hình tam giác.
• Số cạnh của hình chóp tứ giác bằng 8, đó là 4 cạnh bên và 4 cạnh thuộc mặt đáy.
• Đường cao của hình này chính là đoạn thẳng được vẽ theo phương vuông góc từ đỉnh đến mặt đáy.
• Có tổng cộng 5 đỉnh trong một hình chóp tứ giác. Các đỉnh này bao gồm 4 đỉnh cùng thuộc mặt đáy và 1 đỉnh nằm ngoài.
• Khi hình chóp có 4 cạnh bên bằng nhau và mặt đáy là một hình vuông thì đó chính là một chóp tứ giác đều.

 

Các công thức tính toán của hình chóp tứ giác

Khi giải các bài toán về hình chóp tứ giác, bạn sẽ thường gặp các dạng toán tính diện tích và thể tích. Đây là một phần quan trọng trong chương trình học toán và cũng xuất hiện nhiều trong đo lường và thiết kế. Để giúp bạn tiếp cận nhanh chóng với các dạng bài toán liên quan, Sforum đã tổng hợp những công thức quan trọng dưới đây:

Công thức tính diện tích xung quanh

Hình chóp tứ giác ABCD có diện tích xung quanh được xác định bằng cách tính tổng tất cả các mặt bên. Nói cách khác, bạn chỉ cần xác định diện tích của từng tam giác tạo thành mặt bên rồi cộng lại. Công thức chung như sau:

Sxq = S₁ + S₂ + S₃ + S₄

Trong đó:

• Sxq: Ký hiệu thể hiện diện tích xung quanh.
• S₁, S₂, S₃, S₄: Diện tích của 4 mặt tam giác của hình chóp.

Công thức tính diện tích toàn phần

Khi tính diện tích toàn phần của một hình chóp tứ giác ta cần tính tổng diện tích của toàn bộ mặt phẳng của hình chóp đó. Tức là bạn cần xác định diện tích mặt đáy với diện tích xung quanh của hình đó. Công thức chung là:

Stp = Sxq + Sđáy

Trong đó:

• Stp: Ký hiệu cho diện tích toàn phần.
• Sđáy: Ký hiệu diện tích của đáy.
• Sxq: Ký hiệu diện tích xung quanh.

Công thức tính thể tích

Khi tính thể tích hình chóp tứ giác ta cần phải biết chiều cao và mặt đáy của hình. Cụ thể là diện tích của mặt đáy và số đo độ dài chiều cao của hình chóp. Công thức chung khi tính thể tích của hình chóp tứ giác là:

Công thức: V = (Sđáy * h)/3

Trong đó:

• Sđáy: Ký hiệu diện tích của mặt đáy hình chóp.
• V: Ký hiệu thể tích.
• h: Ký hiệu độ dài đường cao.

Bài tập thực hành về hình chóp tứ giác

Để nắm vững kiến thức liên quan đến hình chóp tứ giác, bạn cần luyện tập nhiều với các dạng bài tập khác nhau. Sforum đã tổng hợp một số bài tập và lời giải chi tiết, bạn hãy xem và thực hành ngay nhé!

Bài 1: Một hình chóp S.ABCD có đáy là hình chữ nhật với chiều rộng AD 6cm, chiều dài AB 8cm. Cho cạnh SA có độ dài 10 cm, SA ⊥ (ABCD). Bạn hãy cho biết thể tích hình này là bao nhiêu?

Lời giải:

ABCD là hình chữ nhật => Sđáy = 8 * 6 = 48cm²

Hình chóp S.ABCD có cạnh bên SA⊥ (ABCD) => SA là đường cao

=> V = 1/3*48*10 = 160 cm³.

Bài 2: Hình chóp S.ABCD có ABCD là hình chữ nhật, AB và BC có độ dài lần lượt là a và a√3. Điểm H là trung điểm của AD, (SHC) ⊥ (ABCD) và (SHD) ⊥ (ABCD), góc giữa SD với (ABCD) là 60º. Bạn hãy tính thể tích của hình chóp tứ giác này theo a.

Lời giải:

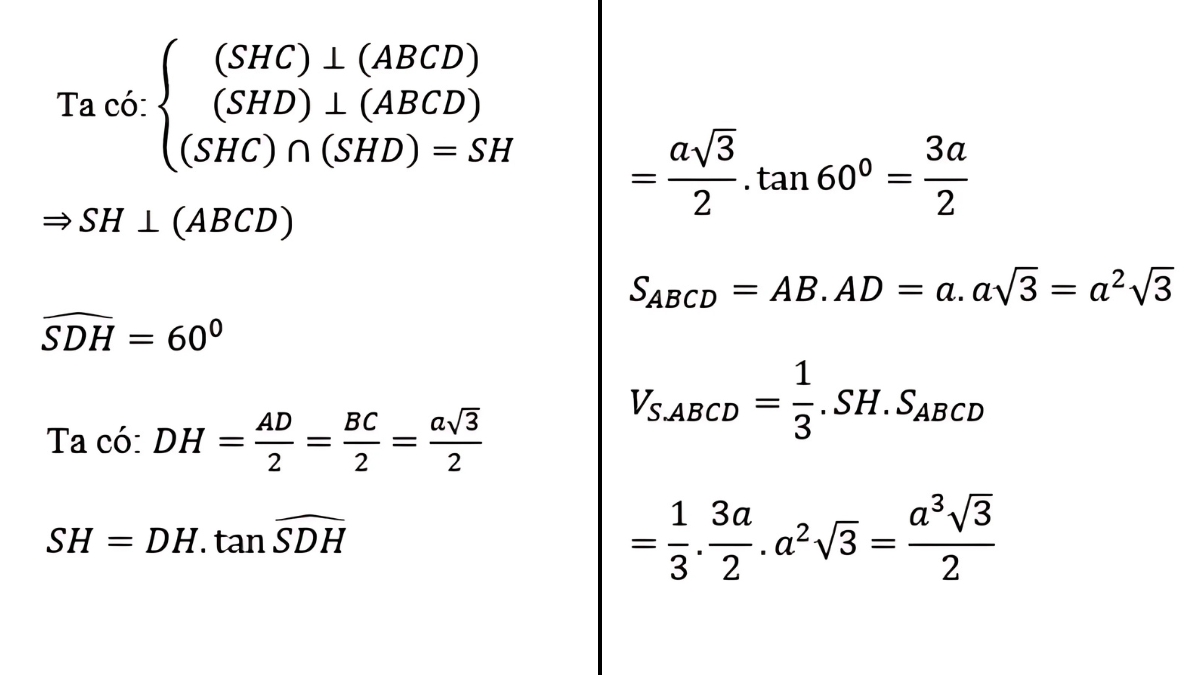
Sforum đã chia sẻ cho bạn những thông tin quan trọng về số cạnh và thể tích của hình chóp tứ giác ABCD. Việc hiểu rõ các kiến thức này sẽ giúp bạn tiếp cận dễ dàng hơn với hình học không gian và ứng dụng vào thực tế một cách hiệu quả. Nếu bạn muốn khám phá thêm nhiều kiến thức hình học thú vị khác, hãy xem thêm các bài viết tiếp theo của Sforum về giáo dục cũng như các chủ đề khác nhé!

Các bài viết cùng chủ đề: Góc Học & Dạy 4.0