Hình hộp chữ nhật: Tính chất, công thức và bài tập liên quan

Diện tích xung quanh, diện tích toàn phần và cách tính thể tích hình hộp chữ nhật là những kiến thức quan trọng trong hình học không gian. Việc hiểu rõ tính chất và công thức liên quan giúp chúng ta dễ dàng giải quyết các bài tập và vận dụng linh hoạt trong cuộc sống. Hãy cùng Sforum bỏ túi những công thức và mẹo làm bài sau đây.
Hình hộp chữ nhật là gì?
Hình hộp chữ nhật là một phiên bản ba chiều của hình chữ nhật, nói cách khác nó là một khối không gian với sáu mặt phẳng vuông góc, đối xứng từng cặp. Mỗi mặt đại diện cho một phần diện tích, được nối kết chặt chẽ bởi các cạnh thẳng và góc vuông đều đặn. Điểm nổi bật của hình này là tính cân đối, dễ dàng tính toán và áp dụng vào thực tiễn.
Hình hộp chữ nhật là khối hình cơ bản trong chuyên đề không gian và dựng hình. Chính vì thế, nó không chỉ biểu thị sự đơn giản mà còn chứa đựng tính ứng dụng đa dạng trong đời sống, chẳng hạn như thiết kế nội thất hay lập trình đồ họa.

Các tính chất cơ bản của hình hộp chữ nhật
Đầu tiên, tất cả các mặt của nó đều là hình chữ nhật và được ghép lại theo từng cặp song song. Tiếp theo, các cạnh của hình hộp chữ nhật giao nhau theo góc vuông, tạo nên các đường thẳng vuông góc chặt chẽ, góp phần giữ vững hình dạng của khối.
Ngoài ra, hình hộp chữ nhật có khả năng chia đều không gian theo từng phần bằng nhau nhờ vào các mặt phẳng đối diện song song và bằng nhau về kích thước. Mỗi đỉnh của hình là nơi giao nhau của ba cạnh, và tất cả các góc tại đỉnh này đều là góc vuông. Chính sự đơn giản này đã giúp nó trở thành mô hình tiêu biểu cho các khối hình học ba chiều.
Một đặc điểm nổi bật nữa của hình hộp chữ nhật chính là các đường chéo của nó. Chúng không chỉ bằng nhau mà còn gặp nhau tại một điểm ở trung tâm hình, tạo nên một liên kết đối xứng hoàn hảo. Đường chéo này đồng thời là công cụ hữu ích trong việc tính toán các thông số không gian của hình.
Cách tính thể tích hình hộp chữ nhật tương đối đơn giản và điển hình, nhờ vào công thức đơn giản nhân chiều dài, chiều rộng và chiều cao. Tính chất này thường được áp dụng trong thực tế, chẳng hạn như đo lường sức chứa hoặc thiết kế các không gian lưu trữ.

Các công thức tính liên quan đến hình hộp chữ nhật
Những công thức này giúp xác định các thông số quan trọng như thể tích, diện tích xung quanh hay diện tích toàn phần hình hộp chữ nhật là những dạng bài không hiếm gặp. Trước khi vận dụng những dạng mở rộng của các thông số này, bạn nên nắm vững những đại lượng quan trong sau
Công thức tính diện tích xung quanh hình hộp chữ nhật
Diện tích xung quanh của hình hộp chữ nhật là biểu hiện của không gian tiếp xúc trực tiếp giữa hình hộp chữ nhật và môi trường bên ngoài, ngoại trừ hai mặt đáy. Công thức này cho thấy diện tích xung quanh phụ thuộc vào chu vi của mặt đáy nhân với chiều cao.
Công thức tính diện tích xung quanh hình hộp chữ nhật: Sxq=2(a+b)h
- a và b lần lượt là chiều dài và chiều rộng của đáy.
- h là chiều cao của hình hộp chữ nhật.
Công thức này được xây dựng dựa trên sự cộng dồn diện tích của từng mặt bên. Điều này thường được ứng dụng trong các trường hợp thực tiễn như tính vật liệu bọc quanh, như giấy gói quà hay tấm cách nhiệt.
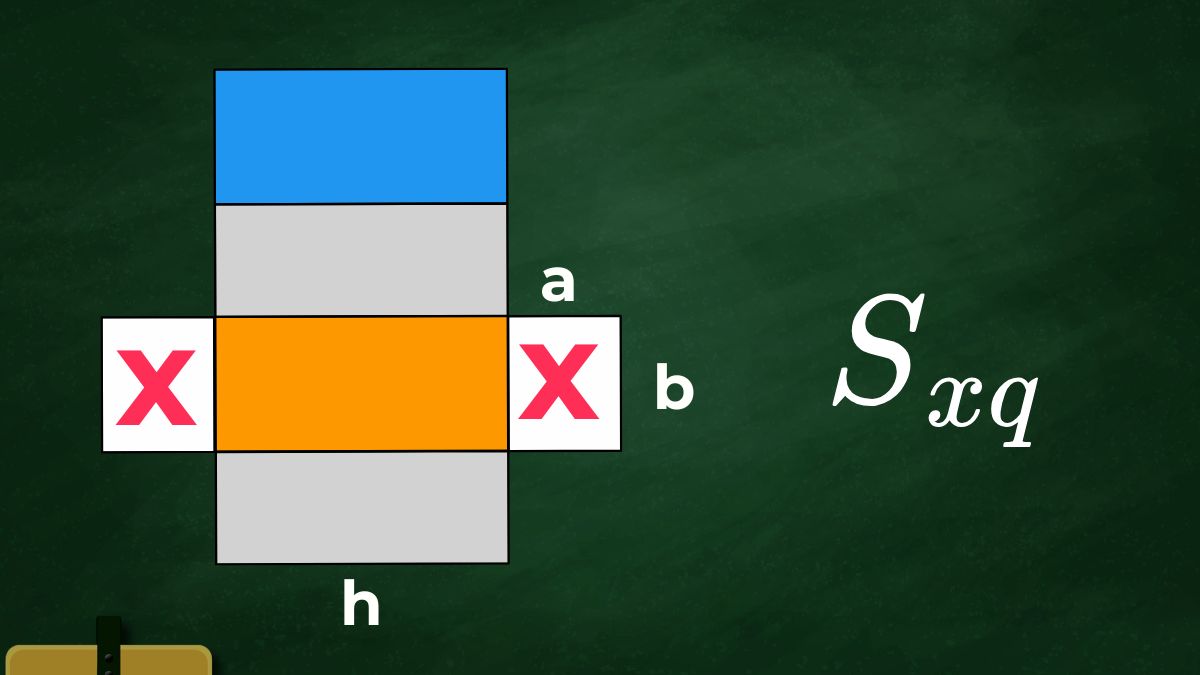
Công thức tính diện tích toàn phần hình hộp chữ nhật
Diện tích toàn phần hình hộp chữ nhật là tổng diện tích các mặt tiếp xúc của hình hộp chữ nhật. Nói khác nó bao gồm diện tích xung quanh và diện tích hai mặt đáy.
Công thức tính diện tích toàn phần hình hộp chữ nhật: Stp=Sxq+Sđáy=2(a+b)h+ 2ab
- a và b lần lượt là chiều dài và chiều rộng của đáy.
- h là chiều cao của hình hộp chữ nhật.
Diện tích toàn phần phản ánh toàn bộ bề mặt của hình hộp chữ nhật, không bỏ sót bất kỳ mặt nào. Đây là con số đại diện cho phạm vi tiếp xúc giữa hình khối và môi trường xung quanh. Bản chất này đặc biệt hữu ích trong việc ước tính nguyên liệu bao phủ, như sơn hay giấy dán, đồng thời là minh họa trực quan cho mối liên hệ giữa các kích thước cơ bản.

Công thức tính thể tích hình hộp chữ nhật
Cách tính thể tích hình hộp chữ nhật dựa trên nguyên tắc cơ bản của hình học không gian: diện tích mặt đáy nhân với chiều cao. Công thức này cho thấy thể tích là sản phẩm của ba kích thước cơ bản, giúp đo lường khả năng chứa đựng của hình khối.
Cách tính thể tích hình hộp chữ nhật: V=abh
- a và b lần lượt là chiều dài và chiều rộng của đáy.
- h là chiều cao của hình hộp chữ nhật.
Thể tích là đặc điểm quan trọng nhất của một khối không gian, biểu thị khả năng chiếm dụng trong thực tế. Bản chất của nó là sự kết hợp hài hòa giữa các chiều đo để tạo nên không gian ba chiều. Giá trị này không chỉ mang tính toán học mà còn ứng dụng thực tiễn, từ việc đo lường sức chứa thùng hàng đến dự đoán nguyên liệu cần thiết cho các công trình.

Một số dạng bài tập cụ thể về hình hộp chữ nhật
Nắm vững các dạng bài tập liên quan đến hình hộp chữ nhật không chỉ giúp rèn luyện tư duy không gian mà còn mở rộng khả năng ứng dụng trong nhiều lĩnh vực. Dưới đây là một số dạng bài tập cụ thể giúp bạn hiểu sâu hơn về khối hình thú vị này.
Dạng 1: Tính diện tích toàn phần của hình hộp chữ nhật
Đề bài 1 (cơ bản): Một hình hộp chữ nhật có chiều dài a=8cm, chiều rộng b=5cm, và chiều cao h=10cm. Hãy tính diện tích toàn phần của hình hộp chữ nhật này.
Cách giải tham khảo:
Áp dụng công thức diện tích toàn phần hình hộp chữ nhật: Stp=Sxq+Sđáy=2(a+b)h+ 2ab
Thay số: Stp=Sxq+Sđáy=2x(8+5)x10 + 2x8x5=340cm2
Đề bài 2 (mở rộng): Một hình hộp chữ nhật có chiều dài a=10 cm, chiều rộng b=6 cm và diện tích toàn phần Stp=376 cm2. Tính chiều cao hhh của hình hộp.
Cách giải tham khảo:
Áp dụng công thức diện tích toàn phần hình hộp chữ nhật: Stp=Sxq+Sđáy=2(a+b)h+ 2ab
Thay số: 376=2x(10+6)h+2x10x6 ⇔ 376=32h+120 ⇔ h = 8 cm

Dạng 2: Tính thể tích của hình hộp chữ nhật
Đề bài 1 (cơ bản): Một bể nước hình hộp chữ nhật có chiều dài a=2 m, chiều rộng b=1.5 m và chiều cao h=1 m. Tính thể tích của bể nước này.
Cách giải tham khảo:
Áp dụng công thức thể tích hình hộp chữ nhật: V=abh
Thay số: V=2x1.5x1=3m3
Đề bài 2 (mở rộng): Một hình hộp chữ nhật có thể tích V=540 cm3 và chiều cao h=9 cm. Biết rằng chiều dài a gấp đôi chiều rộng b. Tìm a và b.
Cách giải tham khảo:
Áp dụng công thức thể tích hình hộp chữ nhật: V=abh và tỷ số a=2b
Thay số: 540=2bxbx9 ⇔ 540=18b2 ⇔ b2=30 ⇔ b= √30 và a=2√30

Dạng 3: Tính diện tích xung quanh của hình hộp chữ nhật
Đề bài 1 (cơ bản): Một chiếc hộp quà có chiều dài a=12 cm, chiều rộng b=8 cm và chiều cao h=15 cm. Hãy tính diện tích xung quanh của chiếc hộp này.
Cách giải tham khảo:
Áp dụng công thức tính diện tích xung quanh hình hộp chữ nhật: Sxq=2(a+b)h
Thay số: Sxq=2x(12+8)x15=600 cm2
Lưu ý, Khi làm bài diện tích xung quanh, toàn phần hay thể tích hình hộp chữ nhật, hãy chú ý đổi sự đồng bộ của đơn vị đo. Đối với những bài phức tạp hơn, bạn nên vẽ hình và chú thích các đại lượng để tránh sai sót. Để có thêm nhiều kinh nghiệm làm bài, bạn có thể tự rèn luyện và kết nối với bạn bè toàn quốc chỉ với chiếc laptop cấu hình tiêu chuẩn sau.
[Product_Listing categoryid="1054" propertyid="" customlink="https://cellphones.com.vn/laptop/sinh-vien.html" title="Tham khảo danh sách laptop sinh viên được quan tâm tại CellphoneS!"]
Diện tích xung quanh, toàn phần và cách tính thể tích hình hộp chữ nhật là nền tảng quan trọng để hiểu sâu hơn về hình học không gian. Qua đó, bạn sẽ nắm được cách mà kiến thức toán giúp ích cho cuộc sống. Bạn còn có thể tìm thấy những công thức toán học quan trọng khác trong cùng chuyên mục về giáo dục của Sforum.
Xem thêm bài viết ở chuyên mục: Mẹo vặt








Bình luận (0)