Tất tần tật thông tin về hình lục giác đều cho bạn

Bạn đã biết cách vẽ, tính chất, diện tích hình lục giác đều chưa? Loại đa giác này không chỉ có nhiều đặc điểm thú vị mà còn xuất hiện phổ biến trong đời sống thực tế. Sforum đã tổng hợp đầy đủ những kiến thức quan trọng trong bài viết này, giúp bạn nắm bắt từ lý thuyết cơ bản đến cách áp dụng, mời bạn cùng xem nhé!

Hình lục giác đều là hình gì?

Hình lục giác đều được biết đến là một đa giác vô cùng đặc biệt với 6 cạnh có cùng độ dài và 6 góc trong bằng 120 độ. Đường chéo của lục giác đều cũng bằng nhau và giao nhau tại tâm đối xứng. Hình này xuất hiện phổ biến trong tự nhiên, từ cấu trúc tổ ong đến các tinh thể. Trong toán học, bạn có thể thấy hình này trong các bài toán về tính diện tích, chu vi và các ứng dụng thực tế trong kiến trúc, nghệ thuật,...

Tính chất của hình lục giác đều

Hình lục giác đều sở hữu một số tính chất thú vị giúp nó trở thành một trong những đa giác đặc biệt nhất, cụ thể là:

• Độ dài của 6 cạnh đều bằng nhau
• Sáu góc trong đều bằng 120 độ
• Các cạnh đối diện đều có tính chất song song
• Những đường thẳng nối từ các đỉnh đối diện nhau đều có số đo bằng nhau
• Tâm đối xứng là điểm giao nhau của các đường chéo chính
• Sáu trục đối xứng là những đường ngang qua tâm và điểm chính giữa các cạnh

Một chiếc iPad với màn hình sắc nét và hiệu năng vượt trội sẽ là công cụ lý tưởng để hỗ trợ học tập, đặc biệt là trong việc giải quyết các bài toán hình học. Nếu bạn đang tìm một thiết bị mới, đừng quên khám phá ngay những mẫu iPad chính hãng từ CellphoneS qua liên kết dưới đây. Tìm hiểu ngay!

[Product_Listing categoryid="944" propertyid="" customlink="https://cellphones.com.vn/tablet/ipad.html" title="Các mẫu iPad đang được quan tâm nhiều tại CellphoneS"]

Các công thức tính toán liên quan tới hình lục giác đều

Hình lục giác đều không chỉ nổi bật với tính đối xứng mà còn gắn liền với nhiều công thức toán học quan trọng. Để nắm được cách tính chu vi, diện tích hình này, bạn hãy theo dõi các công thức mà Sforum vừa tổng hợp dưới đây nhé!

Công thức tính chu vi hình lục giác đều

Tính chất của hình lục giác đều là các cạnh có độ dài bằng nhau nên việc tính chu vi trở nên rất đơn giản. Bạn chỉ cần biết độ dài một cạnh, sau đó nhân với 6 là có ngay chu vi của đa giác này. Công thức chung là:

P = 6a

Trong đó:

• a: Chiều dài của cạnh hình lục giác đều
• P: Chu vi

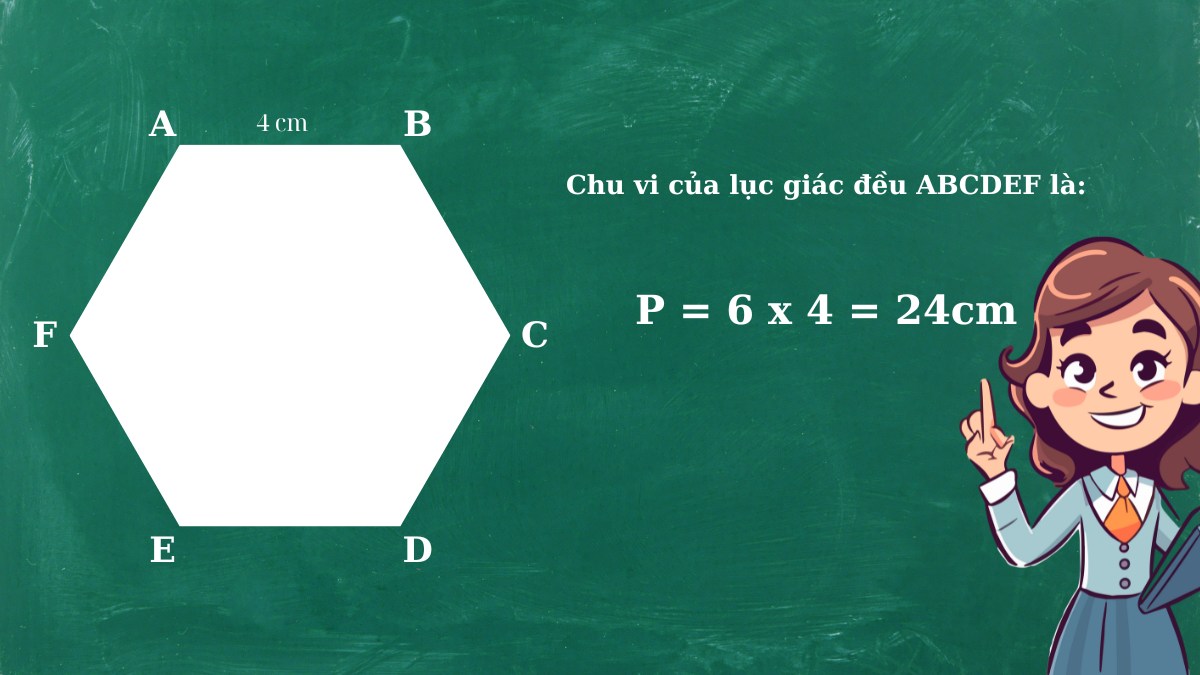
Ví dụ, cho một lục giác đều với các cạnh có độ dài bằng 4cm thì chu vi sẽ là:

P = 6 x 4 = 24cm

Công thức tính diện tích

Tính diện tích hình lục giác đều không chỉ là một bài toán phổ biến trong hình học mà còn được áp dụng nhiều trong đời sống. Với tính chất đối xứng đặc biệt, hình này có một công thức tính diện tích đơn giản. Công thức chung là:

Trong đó:

• S: Diện tích
• a: Độ dài cạnh

Ví dụ: Cho một hình lục giác đều với cạnh bằng 4cm, hãy cho biết diện tích của hình này.

Lời giải:

Diện tích hình lục giác đều này là:

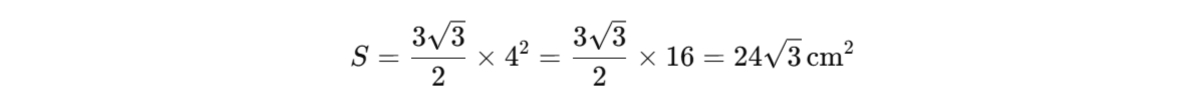
Công thức tính độ dài đường chéo

Một lục giác đều có 6 đỉnh, tạo nên 9 đường chéo, đường chéo chính là những đường được tạo thành bằng cách nối 2 đỉnh đối diện với nhau và có công thức chung là:

d=2a

Trong đó:

d: Độ dài đường chéo chính

a: Độ dài cạnh lục giác đều

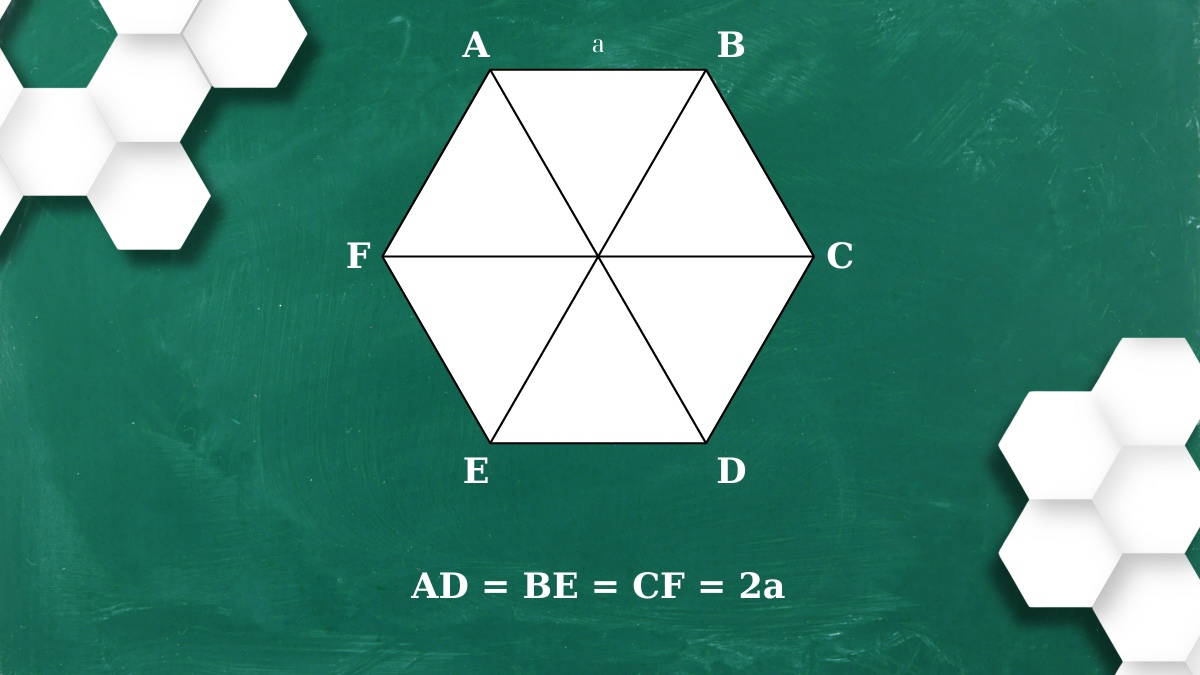
Ví dụ: Hãy cho biết độ dài đường chéo AD từ hình lục giác đều ABCDEF với cạnh bằng 4cm.

Lời giải: AD = 2 x 4 = 8cm

Hướng dẫn vẽ hình lục giác đều nhanh chóng

Cách vẽ hình lục giác đều khá đơn giản, bạn chỉ cần chuẩn bị một số dụng cụ cơ bản như compa, thước thẳng và một cây bút. Chi tiết cách vẽ là như sau:

• Bước 1: Lấy một điểm bất kỳ làm tâm rồi bạn dùng compa vẽ một đường tròn bán kính r.

 

• Bước 2: Giữ nguyên compa, bạn chia đường tròn vừa tạo thành 6 cung tròn bằng nhau.
• Bước 3: Nối 6 điểm vừa chia trên đường tròn bạn sẽ được một hình lục giác đều với độ dài các cạnh bằng r. Đường tròn trên cũng chính là đường tròn ngoại tiếp của hình.
• Bước 4: Nếu bạn chỉ cần vẽ hình lục giác đều thì hãy xóa các đường vẽ nháp đi là hoàn thành.

Một số câu hỏi liên quan

Ở phần trên, Sforum đã giới thiệu đến bạn cách vẽ, tính chất, diện tích hình lục giác đều. Đây đều là những kiến thức quan trọng cần biết khi tìm hiểu về loại đa giác đặc biệt này. Nếu bạn vẫn còn thắc mắc, hãy theo dõi nội dung sau đây để được Sforum giải đáp chi tiết nhé!

Hình lục giác đều có bao nhiêu đường chéo?

Hình lục giác đều sở hữu tổng cộng 9 đường chéo, được xác định cụ thể như sau:

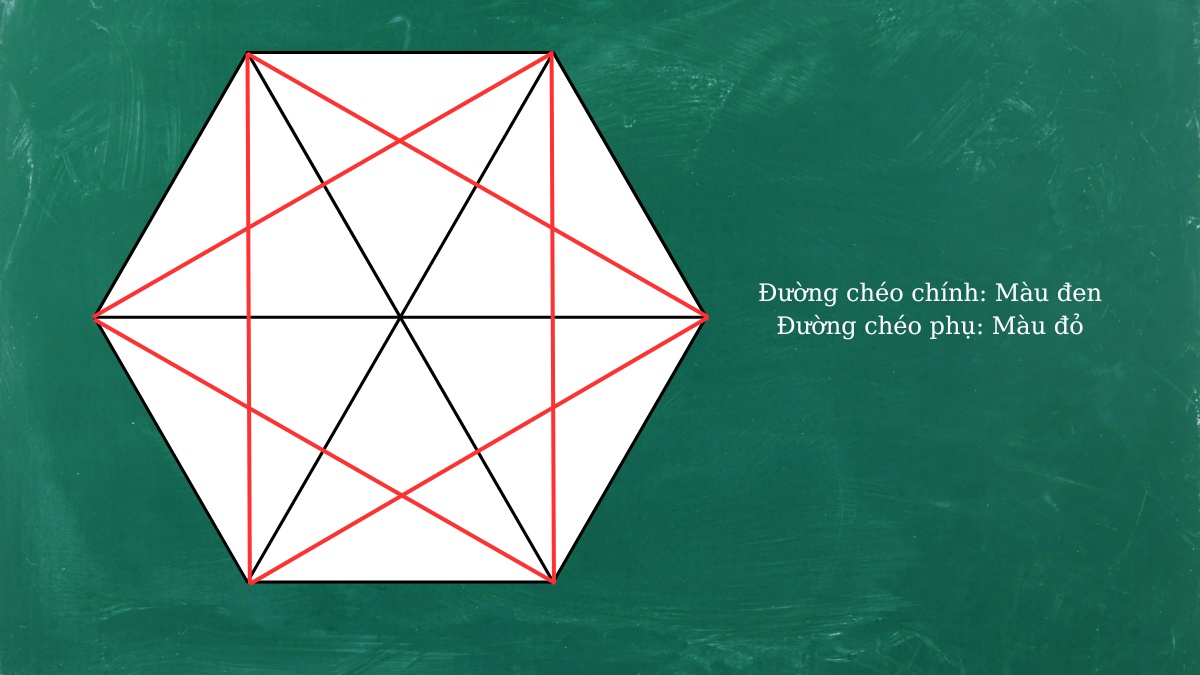
• Đường chéo chính: 3 đường, được tạo thành bằng cách nối 2 đỉnh đối diện. Đường này chia lục giác đều thành 2 nửa bằng nhau, độ dài của nó bằng độ dài đường kính đường tròn ngoại tiếp.
• Đường chéo phụ: 6 đường, được tạo thành khi nối 2 đỉnh không kề nhau (ngoại trừ 2 đỉnh đối diện).

Góc của hình lục giác đều là bao nhiêu độ?

Tất cả các góc của một hình lục giác đều bao giờ cũng bằng 120 độ. Đặc điểm này là yếu tố quan trọng giúp bạn nhận dạng và phân biệt loại đa giác này với các đa giác khác. Một điều thú vị là khi các đường chéo chính chia lục giác đều thành các tam giác thì nó luôn là những hình tam giác đều và bằng nhau.

Hình lục giác đều có bao nhiêu trục và tâm đối xứng?

Hình lục giác đều có sự đối xứng hoàn hảo khi sở hữu 6 trục và 1 tâm đối xứng. Cụ thể là:

• Tâm đối xứng: Chính là điểm cắt nhau của các đường chéo chính, khi bạn xoay hình lục giác đều một góc 60 độ quanh tâm thì sẽ được một hình trùng khít với nó.
• Trục đối xứng: Là những đường ngang qua tâm và trung điểm của một cạnh bất kỳ.

Sforum vừa chia sẻ đến bạn những kiến thức về cách vẽ, tính chất, diện tích hình lục giác đều trong bài viết trên. Mong rằng bạn có thể vận dụng để hoàn thành các bài toán hình học một cách nhanh chóng và hiệu quả. Để biết thêm về những kiến thức bổ ích, mời bạn tiếp tục theo dõi các bài viết cùng chủ đề giáo dục của Sforum nhé!

Đọc thêm bài viết cùng chuyên mục: Góc Học & Dạy 4.0