Tích phân suy rộng - Công thức & Bài tập có lời giải

Trong giải tích, có những bài toán yêu cầu tính diện tích hay thể tích nhưng gặp phải biên vô cực hoặc điểm kỳ dị. Việc nắm vững công thức cách tính tích phân suy rộng giúp bạn giải quyết những trường hợp này dễ dàng hơn. Bài viết sẽ giới thiệu lý thuyết và hướng dẫn qua bài tập tính tích phân suy rộng có lời giải loại 1, 2, giúp bạn áp dụng hiệu quả vào thực tế.

Định nghĩa tích phân suy rộng

Tích phân suy rộng là một loại tích phân xác định, nhưng miền lấy tích phân có thể mở rộng đến vô cực hoặc chứa điểm kỳ dị khiến hàm số không xác định. Khi đó, ta không thể tính theo cách thông thường mà phải dùng công thức tích phân suy rộng, tức là tìm giới hạn để kiểm tra sự hội tụ hoặc phân kỳ. 

Nếu giới hạn tồn tại và có giá trị hữu hạn, tích phân được coi là hội tụ; ngược lại, nếu giới hạn không xác định hoặc tiến tới vô cực, tích phân sẽ phân kỳ. Việc hiểu rõ khái niệm này giúp giải quyết nhiều bài toán thực tế và áp dụng vào các lĩnh vực như vật lý, kỹ thuật và kinh tế.

Máy tính bảng là một thiết bị nhỏ gọn nhưng mạnh mẽ sẽ giúp bạn học tập và làm việc hiệu quả hơn mỗi ngày. Với màn hình cảm ứng linh hoạt, bạn có thể dễ dàng tra cứu tài liệu, giải bài tập tính tích phân suy rộng hay thao tác trên các phần mềm chuyên dụng. Tham khảo ngay!

[Product_Listing categoryid="4" propertyid="" customlink="https://cellphones.com.vn/tablet.html" title="Các mẫu Máy tính bảng đang được quan tâm nhiều tại CellphoneS"]

Tính chất của tích phân suy rộng

Tích phân suy rộng có nhiều tính chất quan trọng giúp xác định tính hội tụ hoặc phân kỳ. Việc hiểu rõ các tính chất này giúp đơn giản hóa quá trình tính toán và áp dụng vào các bài toán thực tế. Dưới đây là hai dạng phổ biến của tích phân suy rộng mà bạn cần nắm kỹ.

Tích phân suy rộng loại 1

Tích phân suy rộng loại 1 xảy ra khi miền lấy tích phân có cận vô cực, tức là dạng [tich-phan-suy-rong-2] hoặc [tich-phan-suy-rong-3]. Để kiểm tra hội tụ, ta sử dụng giới hạn của tích phân trên một khoảng hữu hạn và xét xem giới hạn này có tồn tại hay không. Nếu giới hạn hữu hạn, tích phân hội tụ; nếu giới hạn vô cực hoặc không tồn tại, tích phân phân kỳ.

Tích phân suy rộng loại 2

Tích phân suy rộng loại 2 xuất hiện khi hàm số không xác định tại một điểm trong miền lấy tích phân. Chẳng hạn như dạng [tich-phan-suy-rong-5] với f(x) không xác định tại x = c (a

Để xét hội tụ, ta chia tích phân thành hai phần và lấy giới hạn khi tiến gần đến điểm kỳ dị. Nếu giới hạn có giá trị hữu hạn, tích phân được coi là hội tụ; ngược lại, nếu giới hạn không xác định hoặc tiến đến vô cực, tích phân sẽ phân kỳ.

Điều kiện tích phân suy rộng hội tụ

Khi áp dụng công thức tích phân suy rộng, kết quả có thể hội tụ hoặc phân kỳ tùy theo đặc điểm của hàm số và miền tính toán. Để xác định sự hội tụ, ta xét giới hạn của tích phân trên miền lấy tích phân và áp dụng các tiêu chuẩn hội tụ phù hợp.

Điều kiện tích phân suy rộng hội tụ loại 1

Đối với tích phân suy rộng loại 1, hội tụ xảy ra nếu giới hạn sau tồn tại và hữu hạn: [tich-phan-suy-rong-6]. Nếu giới hạn này hữu hạn, bài tập tích phân suy rộng loại 1 có nghiệm hội tụ; ngược lại, nếu giới hạn tiến đến vô cực hoặc không xác định, kết quả sẽ phân kỳ. Ngoài ra, có thể sử dụng tiêu chuẩn so sánh: nếu f(x) ≤ g(x) với mọi x đủ lớn và [tich-phan-suy-rong-7] hội tụ, thì [tich-phan-suy-rong-8] cũng hội tụ.

Điều kiện tích phân suy rộng hội tụ loại 2

Với bài tập tích phân suy rộng loại 2, hội tụ xảy ra nếu tồn tại giới hạn hữu hạn của tích phân tại điểm kỳ dị: [tich-phan-suy-rong-10] hoặc [tich-phan-suy-rong-11]. Nếu giới hạn tồn tại và hữu hạn, tích phân hội tụ; nếu giới hạn bằng vô cực hoặc không xác định, tích phân phân kỳ. Để kiểm tra hội tụ, có thể áp dụng tiêu chuẩn so sánh tương tự như tích phân loại 1.

Phương pháp tính tích phân suy rộng

Để tính tích phân suy rộng, ta thường áp dụng các phương pháp biến đổi hoặc phân tích để đơn giản hóa bài toán. Hai phương pháp phổ biến là phép biến đổi Laplace, Fourier và khai triển tích phân thành chuỗi.

Phép biến đổi Laplace và phép biến đổi Fourier

Phép biến đổi Laplace giúp chuyển một tích phân khó tính về miền tần số, giúp đơn giản hóa phép tính bằng cách sử dụng bảng biến đổi chuẩn có sẵn. Phép biến đổi Fourier cũng có vai trò tương tự, đặc biệt hữu ích khi xử lý các hàm dao động hoặc có dạng xung. Cả hai phương pháp này đều được áp dụng rộng khắp trong các lĩnh vực như khoa học tự nhiên, công nghệ và xử lý tín hiệu.

Khai triển tích phân thành chuỗi

Một số tích phân suy rộng có thể được biểu diễn dưới dạng tổng của một chuỗi số. Bằng cách khai triển hàm dưới dấu tích phân thành chuỗi, ta có thể đánh giá từng thành phần riêng lẻ và tính toán dễ dàng hơn. Phương pháp này thường hữu ích khi hàm số có thể khai triển theo chuỗi Taylor hoặc chuỗi Fourier, giúp xác định nhanh sự hội tụ của tích phân.

Bài tập tích phân suy rộng có lời giải

Dưới đây là ba bài tập tích phân suy rộng có lời giải giúp bạn hiểu rõ hơn về các dạng phổ biến.

Bài 1: Bài tập tích phân suy rộng loại 1 (cận vô hạn)

Tính tích phân suy rộng:

=> Lời giải cho bài tập tích phân suy rộng loại 1:

Sử dụng công thức tích phân suy rộng loại 1, ta viết: [tich-phan-suy-rong-14]

Tính tích phân xác định:

Lấy giới hạn khi b → ∞:

Vậy tích phân hội tụ và có giá trị:

Bài tập 2: Bài tập tích phân suy rộng loại 2 (hàm không bị chặn) 

Tính tích phân suy rộng:

=> Lời giải: 

Đây là bài tập tích phân suy rộng loại 2 vì hàm số [tich-phan-suy-rong-20] không bị chặn tại x = 0. 

Áp dụng cách tính tích phân suy rộng, ta viết:

Tính tích phân xác định:

Lấy giới hạn khi a → 0+:

Vậy tích phân hội tụ và có giá trị:

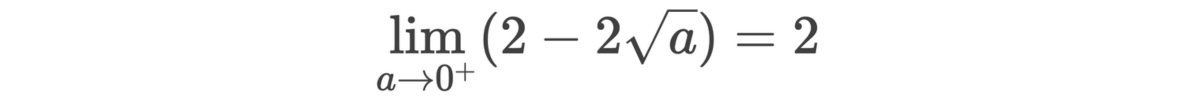
Bài tập 3: Bài tập tính tích phân suy rộng kết hợp (cận vô hạn và hàm không bị chặn) 

Tính tích phân suy rộng:

=> Lời giải: 

Đây là bài tập tích phân suy rộng kết hợp cả loại 1 và loại 2. Hàm số [tich-phan-suy-rong-26] không bị chặn tại x = 0 và có cận vô hạn tại x = ∞. Ta chia tích phân thành hai phần: [tich-phan-suy-rong-27]

Xét tích phân 

Khi a → 0+,

nên tích phân này phân kỳ. 

Xét tích phân

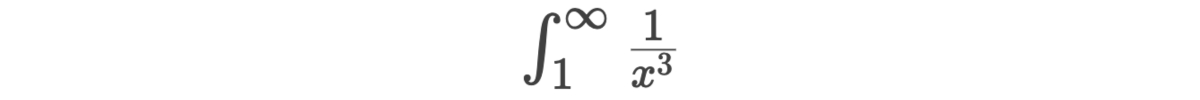
Tích phân này hội tụ.

Kết luận của bài tập tích phân suy rộng có lời giải này là: Vì một phần của tích phân phân kỳ, nên tích phân ban đầu phân kỳ.

Việc vận dụng thành thạo công thức cách tính tích phân suy rộng sẽ giúp bạn giải quyết nhiều bài toán phức tạp trong giải tích. Qua các bài tập tính tích phân suy rộng có lời giải loại 1, 2, hy vọng bạn có thể áp dụng linh hoạt và tự tin hơn khi gặp dạng toán này. Hãy tiếp tục rèn luyện với nhiều bài tập khác để nắm vững hơn về chủ đề này nhé!