Hàm Hyperbolic là gì? Công thức và cách sử dụng hàm Hyperbolic

Hàm Hyperbolic được Vincenzo Riccati và Johann Heinrich Lambert độc lập đưa ra vào những năm 1760. Đây là hàm số có nhiều ứng dụng trong biểu diễn và làm rõ những tính chất của cách hàm lượng giác với một hình thức khác. Hãy cùng Sforum tìm hiểu chuyên sâu về hàm trong toán phổ thông ngay trong bài viết này:

Xem thêm: Đạo hàm 1/x là gì? Các dạng bài tập về đạo hàm

Hàm Hyperbolic là gì?

Hàm Hyperbol là hàm có chức năng tương tự hàm số lượng giác. Nếu các hàm số lượng giác được biểu diễn trên một đường tròn với đơn vị chuẩn thì Hyperbolic được biểu diễn bằng các đường Hyperbol.

Ngoài ra, theo quan điểm toán học Logarit thì hàm Hyperbolic hàm phân thức của ex với điều kiện tử và mẫu số có bậc không lớn hơn 2.

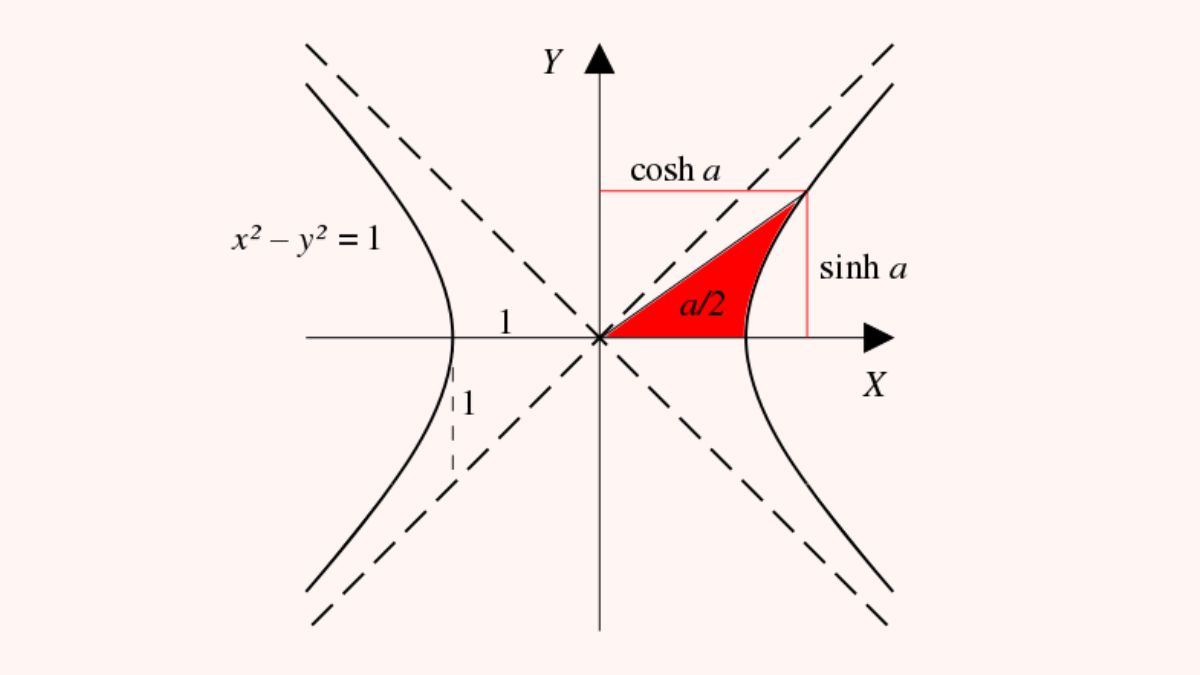
Công thức hàm Hyperbolic

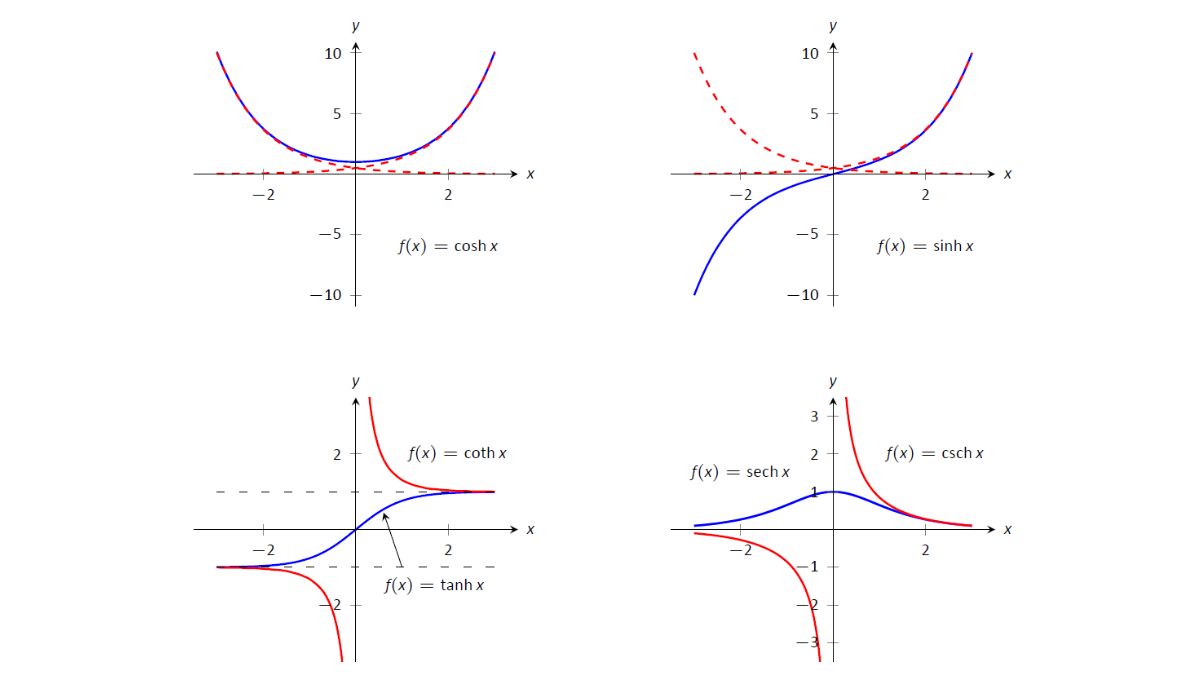
Hàm Hyperbolic có các công thức cơ bản như sin hyperbolic - kí hiệu: sinh; cosin hyperbolic - ký hiệu - cosh và hàm tang hyperbolic - ký hiệu tanh. Từ 3 công thức cơ bản sẽ có những hàm số mở rộng như cotang hyperbol - ký hiệu coth ,sec hyperbol - ký hiệu sech, cosec hyperbol -csch. Sau đây là những công thức cụ thể để xác định:

Các công thức quan trọng của hàm Hyperbolic ngược:

• Công thức hàm sinh: Sinh x = ex-e-x2- là hàm lẻ, đồ thị hàm số đối xứng qua trục hoành
• Công thức hàm cosh: Cosh x =ex+e-x2 - là hàm chẵn, đồ thị hàm số đối xứng qua trục tung
• Công thức hàm tanh: Tanh x = sinh xcosh x- là hàm lẻ, đồ thị hàm số đối xứng qua trục hoành.
• Công thức hàm coth: Coth x = cosh xsinh x- là hàm lẻ, đồ thị hàm số đối xứng qua trục hoành
• Công thức hàm sech: Sech x =1cosh x - là hàm chẵn, đồ thị hàm số đối xứng quan trung tung
• Công thức hàm csch: Csch x =1sinh x - là hàm lẻ, đồ thị hàm số đối xứng qua trục hoành.

Giữa các hàm số hyperbol vẫn có thể thực hiện những phép tính như cộng các đối số, công thức trừ các đối số và công thức tính một nửa đối số.

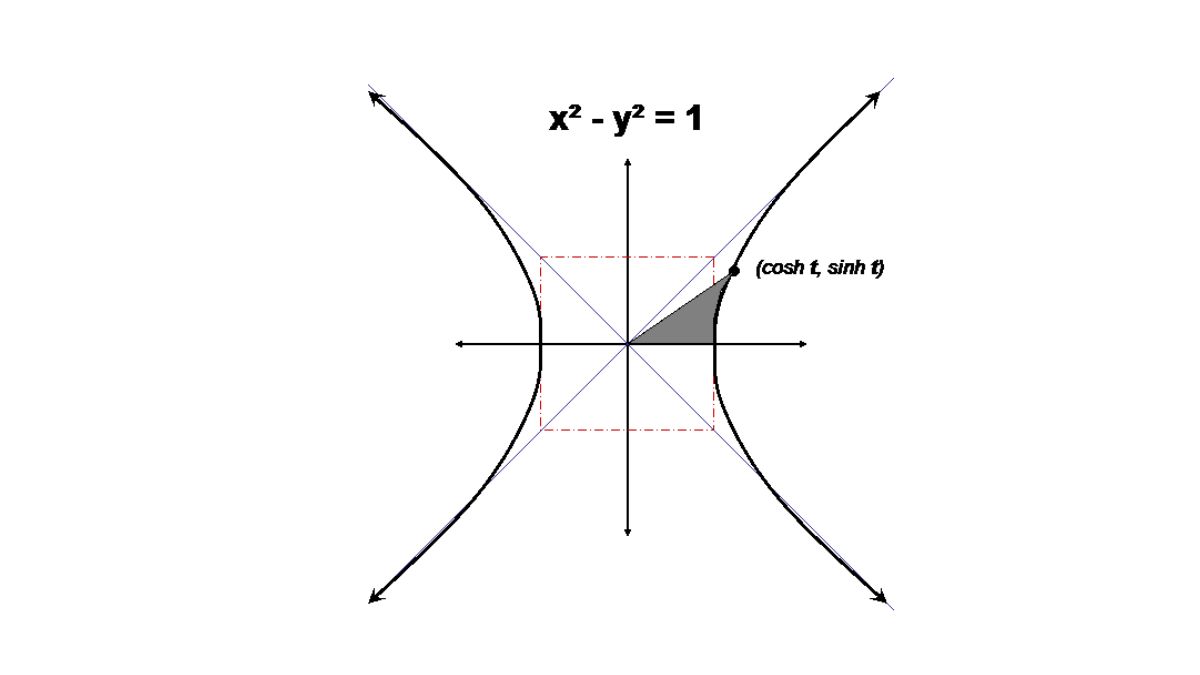
Hàm Hyperbolic ngược

Hàm Hyperbolic ngược, là hàm suy ngược lại từ hàm Hyperbolic. Hay còn gọi là Hyperbolic nghịch đảo. Trong nhiều trường hợp khách Hyperbolic ngược còn được gọi là “hàm diện tích” để nhận ra góc hyperbol.

Với mỗi điểm A (x1,y1) thuộc đồ thị Hyperbolic bạn luôn thu được góc tương ứng AOx, độ lớn của góc này đại diện cho Hyperbolic ngược.

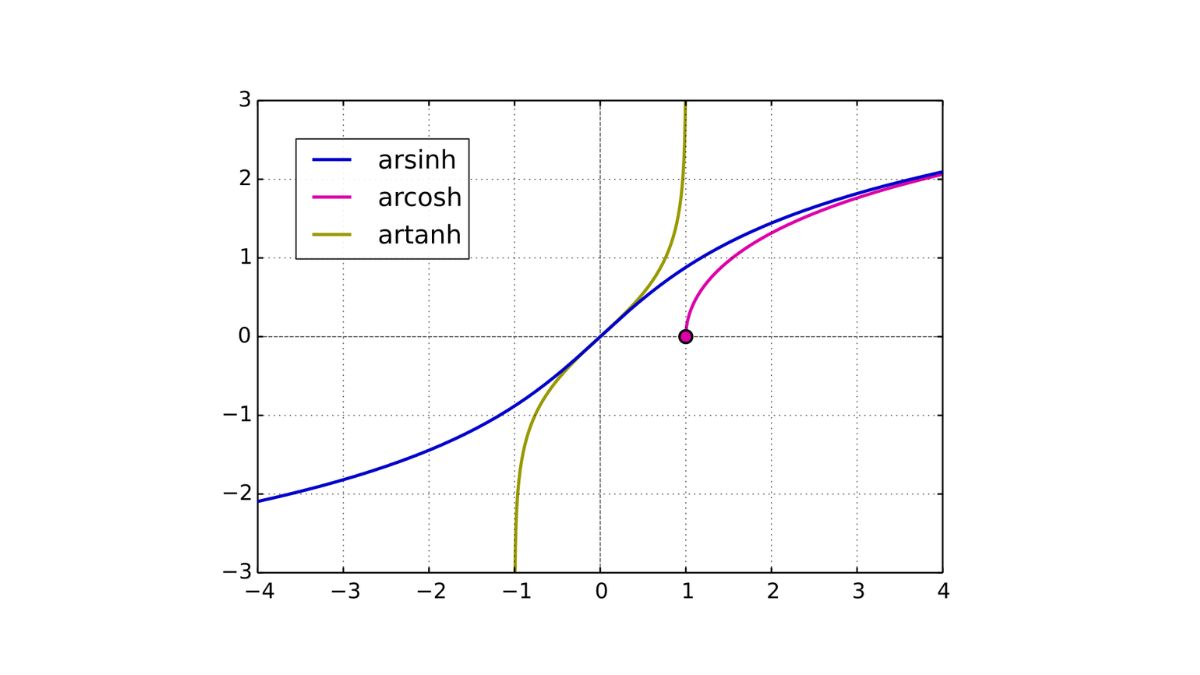
Các công thức quan trọng của hàm Hyperbolic ngược:

• Công thức hàm sinh: Arsinh x =ln(x + x2+1 )
• Công thức hàm cosh: Arcosh x =ln(x + x2-1 )
• Công thức hàm tanh: Artanh x = 12ln(1+x1-x)
• Công thức hàm coth: Arcoth x = 12ln(x+1x-1)
• Công thức hàm sech: Arcech x =ln(1+1-x2x)
• Công thức hàm csch: Arcsch x = ln(1x+1x2+1)

Với một số công thức có mẫu số chứa x, bạn phải tiến hành đặt điều kiện xác định trước khi tính toán.

Hàm Hyperbolic cho số phức

Vận dụng sự liên hệ mật thiết giữa làm Hyperbolic vào hàm mũ được thể hiện qua đồng nhất thức sau:

ex=cosh x + sinh x và e-x=cosh x - sinh x

Từ đó bạn có thể mở rộng cách biểu diễn hàm Hyperbol dưới một hình thức số phức như sau:

Ví dụ hàm Hyperbolic

Hàm Hyperbol có nhiều ứng dụng và cách tính khách nhau. Để hiểu rõ hơn về những ứng dụng thực tế này, mời bạn tham khảo một số ví dụ các đẳng thức và tìm số hạng tổng quát của dãy số bằng hàm Hyperbol.

 

Câu hỏi thường gặp về hàm Hyperbolic

Hàm Hyperbolic là một hàm số nâng cao có nhiều ứng dụng. Vì thế khi ứng dụng, bạn thường có những thắc, hãy cùng tham khảo những câu hỏi thường gặp ngay sau đây.

Đạo hàm của các hàm Hypebolic

Đạo hàm của các hàm Hypebol chính là đạo hàm của các công thức tiêu biểu của nó:

• (sinh x)’ = cosh x
• (cosh x)’ = sinh x
• (tanh x)’ = 1 -tanh2x=sech2x=acosh2x
• (coth x)’ = -coth x.csch x
• (sech x)’= -tanh x.sech x

Bằng ứng dụng các công thức đạo hàm cơ bản của hàm hypebol bạn có thể triển khai những đặc thức phức tạp hơn.

 

 

Cách khai triển hàm Hyperbolic bằng chuỗi Taylor

Chuỗi Taylor của một hàm số là tổng các phần từ kéo dài vô hạn, thu được khi bạn tiến hành lấy đạo hàm của một hàng số tại một điểm. Tổng đó được viết gọn dưới dạng:

 

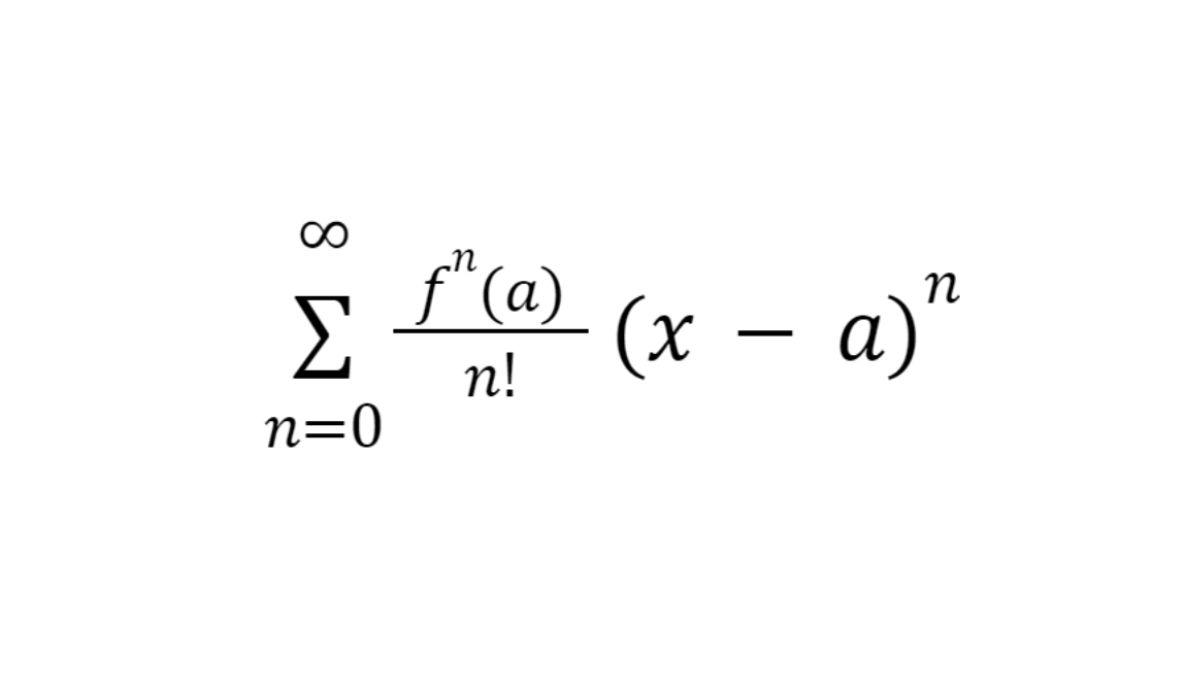
Trong đó, n là bậc của đạo hàm, a là điểm mà tại đó bạn lấy đạo hàm.

Dựa vào lý thuyết đó, có các cách triển khai các công thức của Hyperbolic theo chuỗi Taylor được thể hiện như sau:

• sinh x = x + x33!+ x55! + x77! +.....=n=0x2n+1(2n+1)!
• cosh x = x + x22!+ x44! + x66! +.....=n=0x2n(2n)!
• Tanh x = x - x33+ 2x515 - 17x7315 +.....=n=022n(22n-1)B2nx2n-1(2n+1)!, điều kiện |x| < 2
• Coth x = x-1+ x3- x345 + 2x5945 +.....=n=022n.B2nx2n-1(2n)!, điều kiện 0<|x|<
• Sech x = 1 - x23+ 5x424 - 61x6710 +.....=n=0E2nx2n(2n)!, điều kiện |x| < 2
• Csch x = x-1- x6+ 7x3360 - 31x515120 +.....=n=02(1-22n-1).B2nx2n-1(2n)!, điều kiện 0<|x|<

Trong đó B và E lần lượt kí hiệu của số Bernoulli và Euler.

Trên đây là tổng hợp của Sforum về các lý thuyết của hàm Hyperbolic. Từ đó bạn có thể áp dụng những tính chất của chúng, không chỉ trong toán học mà còn ở các lĩnh vực khác.