Hàm ngược là gì? Tính đạo hàm hàm ngược

Hàm ngược là gì?
Hàm ngược còn được gọi là hàm nghịch đảo (khác với hàm nghịch biến). Về cơ bản, hàm này được hiểu nôm na là một hàm có chứa biến là kết quả của một hàm khác.Về định nghĩa trong môn toán, hàm ngược là việc hoàn tác lại những gì đã được tính của một hàm. Nếu hàm f có hàm nghịch đảo tương ứng thì ta gọi hàm f khả nghịch. Hàm nghịch đảo của hàm f được ký hiệu là f-1.
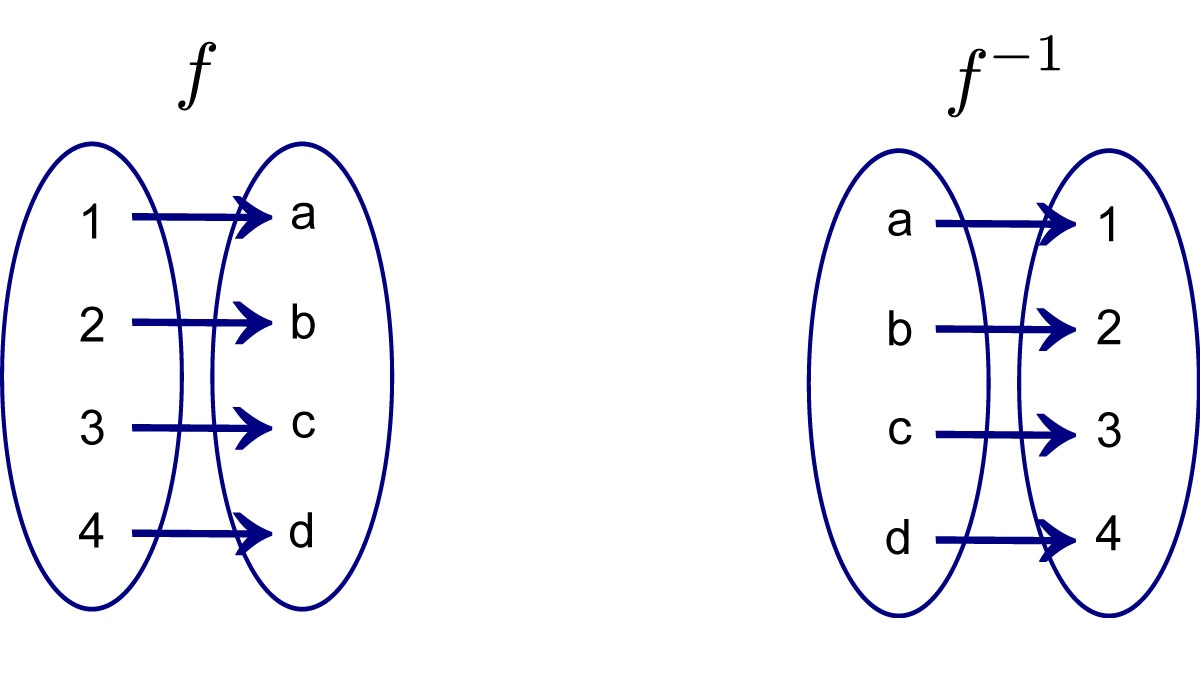
Điều kiện để hàm f khả nghịch chính là song ánh. Điều này có nghĩa là với hai tập X và Y đã cho, với mỗi giá trị x thuộc tập X, ta chỉ tìm được một giá trị y tương ứng thuộc tập Y. Khi đó, mối quan hệ này được biểu diễn như sau:
- f(x) = y
- f-1(y)=x
Trong đó, f(x) là hàm chứa biến x đã cho, còn f-1(y) là hàm nghịch đảo của hàm f(x) theo biến y.
Từ mối quan hệ trên, hàm nghịch đảo của f(x) sẽ được biểu diễn ở dạng tổng quát như sau:
f-1(y) = (phần tử duy nhất x ∊ X sao cho f(x) = y) Xem thêm: Hàm Hyperbolic là gì? Công thức và cách sử dụng hàm Hyperbolic
Công thức tính hàm ngược
Với một số hàm cơ bản như ex, 2x,..., việc tìm hàm nghịch đảo sẽ khá lâu. Nhằm rút ngắn quá trình tính toán, bạn có thể tra bảng sau để tìm hàm ngược tương ứng. Để áp dụng công thức thành công, bạn cần chú ý đến phần điều kiện. Nếu hàm không thỏa điều kiện thì chúng không khả nghịch.
| Hàm f(x) | Hàm ngược f-1(y) | Điều kiện |
| ax + b | (y - )/ba | a ≠0 |
| 1/x | 1/y | x, y ≠0 |
| xa | ya | x, y ≥ 0, p ∈ Z+ |
| 2x | lby | y 0 |
| ex | lny | y 0 |
| 10x | logy | y 0 |
| ax | logay | y 0 và a 0 |
| xex | W(y) | x ≥- 1 và y ≥ -1/e |
| sin(x) | arcsin(y) | -π/2 ≤ y ≤ π/2 |
| cos(x) | arccos(y) | 0 ≤ y ≤ π |
| tan(x) | arctan(y) | -π/2 < y < π/2 |
| cot(x) | arccot(y) | 0 < y < π |
| sec(x) | arcsec(y) | 0 < y < π và y ≠ π/2 |
| csc(x) | arccsc(y) | -π/2 < y < π/2 và y ≠ 0 |
| sinh(x) | arsinh(y) | |
| cosh(x) | arcosh(y) | y 1 |
| tanh(x) | artanh(y) | |y| < 1 |
| coth(x) | arcoth(y) | |y| 1 |
| sech(x) | arsech(y) | 0 < y ≤ 1 |
| csch(x) | arcsch(y) |
Các ví dụ về hàm ngược cơ bản
Để giúp bạn hiểu rõ hơn về hàm nghịch đảo, Sforum sẽ đưa ra một số ví dụ cụ thể như sau:
Hàm bậc nhất
Mỗi hàm bậc nhất luôn luôn có một hàm nghịch đảo tương ứng, hay có thể nói mọi hàm bậc nhất đều khả nghịch. Xét ví dụ với hàm f(x) = 2x - 3. Khi đó, hàm nghịch đảo của f(x) = 2x - 3 là f-1(y) = (y + 3)/2.

Hàm bình phương
Mọi hàm bình phương đều không khả nghịch trên miền giá trị R. Để khả nghịch, bạn buộc phải xét hàm bình phương trên khoảng giá trị không âm. Với hàm f(x) = x2 có miền giá trị [0,) thì hàm f-1(y) = y.
Xem thêm: Đạo hàm 1/x là gì? Các dạng bài tập về đạo hàmCách tính đạo hàm hàm ngược
Trước khi tính đạo hàm của hàm nghịch đảo, bạn cần xét tính khả vi của hàm. Nếu hàm f khả vi trên khoảng A thì hàm nghịch đảo của hàm f, tức f-1, sẽ khả vi trên khoảng f(A). Theo định lý hàm ngược, đạo hàm của hàm này được tính theo công thức tổng quát:
(f-1)'(y) = 1/(f'(x))

Tính chất của hàm ngược
Hàm nghịch đảo có một số tính chất cơ bản dựa vào bản chất hàm. Bạn có thể dựa vào chúng để áp dụng và giải các bài toán.
Tính duy nhất
Mỗi hàm f xác định chỉ có duy nhất một hàm nghịch đảo f-1 tương ứng. Ngược lại, mỗi hàm f-1 cũng chỉ có duy nhất một hàm f tương ứng.
Tính đối xứng
Hàm f và hàm ngược của hàm f có tính đối xứng với nhau. Tính chất này thể hiện rõ nhất qua đồ thị của hai hàm trên hệ trục Oxy.
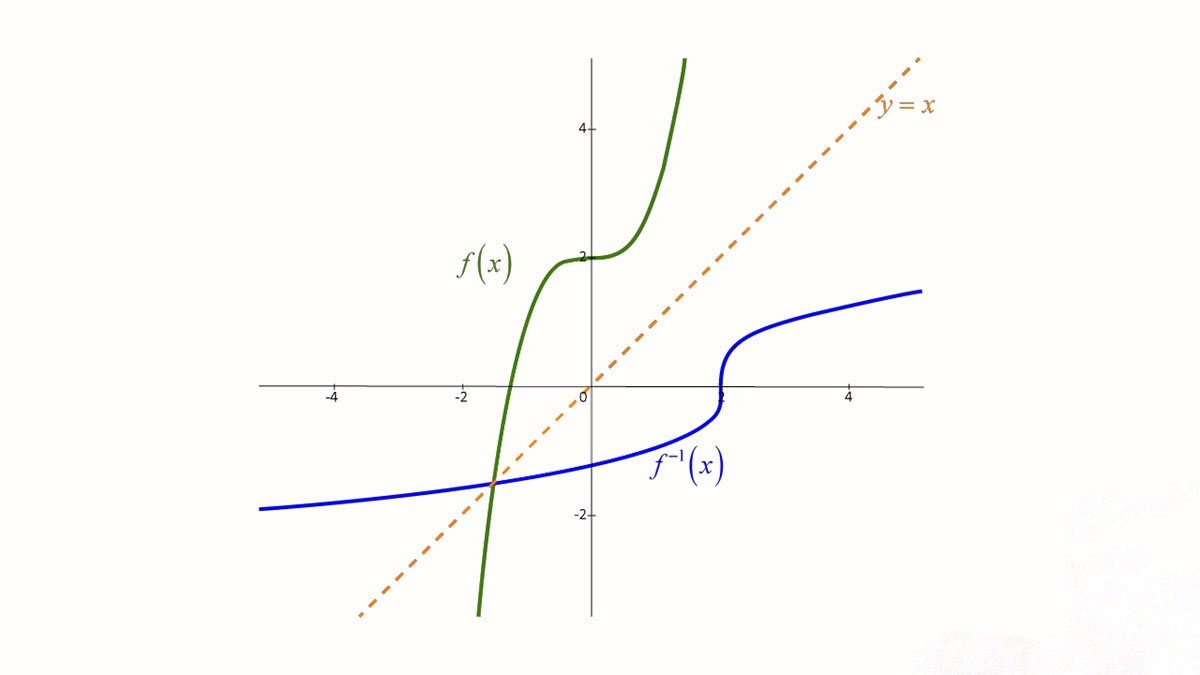
Đồ thị của hàm ngược
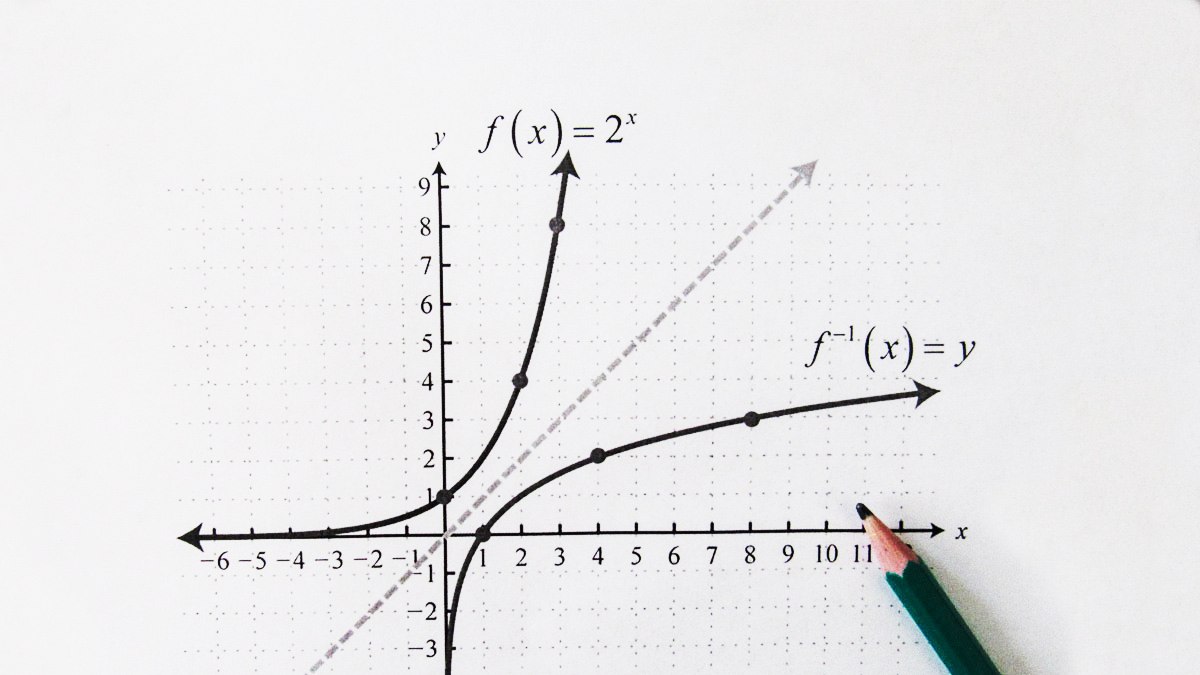
Sau đây là đồ thị biểu diễn hàm nghịch đảo của hàm 2x:
Hàm tự nghịch đảo
Về bản chất thì đây là hàm đồng nhất. Khi biểu diễn trên đồ thị, hàm tự nghịch đảo chính là trục đối xứng của chính nó và các hàm khác. Hàm y = x là một trong những hàm tự nghịch đảo đã được công bố.
Cách xử lý hàm ngược
Để tính toán hàm nghịch đảo, bạn cần áp dụng quy tắc làm và công thức. Nội dung sau đây Sforum không chỉ cung cấp cho bạn hai tài nguyên này mà còn hướng dẫn tìm đạo hàm của hàm nghịch đảo.
Các bước cơ bản để tính hàm ngược
- Bước 1: Đưa hàm đã cho về dạng y = f(x).
- Bước 2: Xét điều kiện song ánh của hàm f(x).
- Bước 3: Nếu thỏa điều kiện thì biến đổi về dạng x = f(y).
- Bước 4: Kết luận.
Cách tìm hàm lượng giác nghịch đảo
Với hàm lượng giác nghịch đảo, bạn cũng làm theo các bước cơ bản nêu trên. Tuy nhiên, lưu ý các giá trị của hàm luôn nhỏ hơn 1 hoặc là dạng radian.
Các bài tập về hàm ngược có lời giải
Bài tập 1: Tìm hàm nghịch đảo của hàm f(x) = ln (x + 3)
Lời giải:
Điều kiện x (-3;∞)
Ta có: ln (x + 3) = y
⇔ x + 3 = ey ⇔ x = ey - 3 Vậy hàm nghịch đảo của hàm f(x) = ln (x + 3) là f-1= ey - 3.
Bài tập 2: Cho f(x) = (3x + 2)/(x+1). Hãy tìm hàm nghịch đảo của hàm trên
Lời giải:
Điều kiện x ≠ -1
Ta có: (3x + 2)/(x+1) = y
⇔ 3x + 2 = y (x + 1)
⇔ 3x + 2 = yx + y
⇔ 3x - yx = y - 2
⇔ x (3 - y) = y - 2
⇔ x = (y - 2)/(3-y)
Vậy hàm nghịch đảo của hàm f(x) đã cho là f-1 = (y - 2)/(3-y).









Bình luận (0)